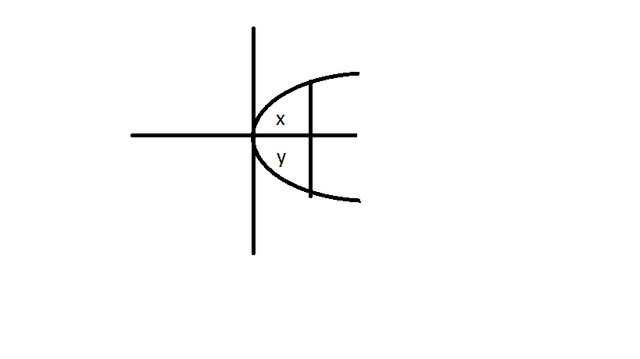Mark44 said:
I wasn't sure that the vertical line you drew was a boundary for the region. You didn't identify that line, as a boundary. Also, when you said this in the first post -- -- that made me think that the vertical line was not a bound on the region. For a region to have a finite area, there need to be boundaries at top and bottom, as well as left and right.
Rumpelstiltskin said:
But the vertical line is an defined limit of x, not y.
No, the vertical line is a boundary of the region you're integrating. I don't think that calling it a "defined limit of x" helps you understand things.
Rumpelstiltskin said:
What I meant by the infinite area was that, if you didn't have the (ostensibly) defined limits of y=0 and/or y = f(x), you'd have infinite area in that case.
Well, if you didn't have those boundaries, you wouldn't have anything to integrate. In any case, if there was no right-hand bound on the region, the area between the graph of f and the x-axis would be infinite.
Rumpelstiltskin said:
Those are usually stated in the problem description if they are looking for the area between the graph of y = f(x) and the x-axis.
Haha, sorry about the miscommunication - I'm not a very rigorous mind. By "who" I was being ironic and pointing out that, since the y limits aren't apparently defined, it looks like someone's just assumed them for their own intentions of finding the area between y = 0 and y = f(x).
What I mean to ask is, why are the y limits always taken to be y = 0 and y = f(x) when integrating?
They aren't, necessarily. It depends on the problem statement and the region whose area you are supposed to find. If the problem asks you to "find the area between the x-axis and the graph of y = f(x), between x = a and x = b" then the integral will be ##\int_{x = a}^b f(x)dx##. It's as simple as that.
If the problem asks you to "find the area between y = 2 and y = f(x), between x = a and x = b" then the integral will be ##\int_{x = a}^b (f(x) - 2)dx##.
Rumpelstiltskin said:
This must be something inherent to the integral.
##\int_{x = 0}^1 (f(x) - 1) dx##. Here I'm assuming that the graph of f lies above the line y = 1 throughout the interval [0, 1]. If that's not the case, things are a bit more complicated.
That makes sense, but it still begs the above question.
I don't see how. I've explained it as clearly as I can.
Rumpelstiltskin said:
The integral ##\int_{x = 0}^1 (f(x) - 0) dx = \int_{x = 0}^1 f(x)dx## implies that the upper limit of the region is the graph of y = f(x) and the lower limit is the line y = 0 (the x-axis).
Yes! Why? How?
You can read it off directly from the first integral I wrote, ##\int_{x = 0}^1 (f(x) - 0) dx ##
The interval over which integration is done is [0, 1], represented by the limits of integration.
Typical area element is ##(f(x) - 0)\Delta x##, which represents the y-coordinate at the top of the area element - the y-coordinate at the bottom of the strip. The typical area element is almost identical to the integrand, with the only difference being ##\Delta x## in the typ. area element vs. dx in the integral.
Rumpelstiltskin said:
The area of the typical area element would be (<y-value at top of curve> - <y-value at bottom of curve>) * ##\Delta x.## Or you could integrate using horizontal strips.
I know. Imagine that in the graph I drew, the parabola was moved up a couple units in relation to the axes, such that the region x (we've since decided that
a would be more appropriate) would be larger than area y (now
b). If I integrated y = f(x), I'd get the area of the region a -- at least that's what we all got in class. Why?
##\int_{x = 0}^1 (f(x) - 0) dx = \int_{x = 0}^1 f(x)dx##Why not also b, since that is also between y = 0 and y = f(x)?
[/quote]You're oversimplifying here. Because of the orientation of the graph (a parabola opening to the right), you don't just simply "integrate y = f(x)."
To quantify things a bit, let's suppose that your graph is the equation ##(y - 2)^2 = x##. This does NOT represent y as a function of x because for each x > 0, there are two y values.
What is region A? (Let's not use either x or a to label the region.) Is it the region inside the parabola and above the x-axis? That does not define a region with finite area. To make a region with a finite area you need a boundary on the right.
I think this problem is well beyond your current abilities, so I think the best thing is for you to hold off until you know more about setting up integrals.