Hello Chemist,
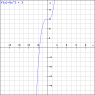
Lets say the velocity function is given as in graph.png (replace f(x) with v and x represents time, ignore negative x).
##
v = 5x^3 + 3
##
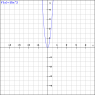
The acceleration function is differentiation of the velocity function as shown in graph(1).png
##
a = 15x^2
##
Now let's go in reverse. Say you are given the acceleration function ##a = 15x^2 ## how will you find the velocity function?
using integration of course.
##
v = \int a \, dx = \int 15x^2 \, dx = 5x^3
##
do you notice that the above velocity function is missing something (i.e. +3) we want our velocity function to be ## v = 5x^3 + 3## but if we derive the velocity function from acceleration function we cannot know what the constant will be so we just add an unknown c. so it should be ## v = 5x^3 + c ##
The constant c can be calculated from knowing initial conditions of the velocity function. e.g. if the question says, at time = 0 (i.e. x = 0) v was 3 then by substituting these values into the above equation (## v = 5x^3 + c ##) you will calculate c as 3 (## c = 3 - 5(0)^3 ##).
what we just performed is indefinite integral (without any boundary to integrate like x
1 to x
2 ).
Now let's say, given the
velocity function can we find the distance traveled
in-between any point in time? e.g. from x = 0.2 to 0.5
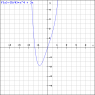
## v = 5x^3 + 3 ## first we integrate and we will get the distance function, graph(2).png ## d = \frac{5}{4}x^4 + 3x ## then find the difference in distance (i.e. d(0.5) - d(0.2)) for x = 0.5 and x = 0.2. notice I did not add +c in the above ## d = \frac{5}{4}x^4 + 3x ## equation because when I subtract d(0.5) - d(0.2) the c will cancel out as it remains unaltered by x. graph(2).png has c = 0 because of the initial condition d = 0 for x = 0.
when you integrate between two points you get the area under the curve between the two points. When the velocity function was integrated it gave the distance traveled by an object between two points although the velocity was changing instantaneously.
Graphs plotted with
http://rechneronline.de/function-graphs/