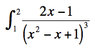Definite Integral with tricky deniminator

kf00zy
Messages
4
Reaction score
0

Homework Statement



I attached problem as a picture.

Homework Equations



I know that the integral of 1/x equals lnx if the derivative of the denominator is equal to the numerator.

The Attempt at a Solution



I tried to foil out the denominator and integrate by parts but it was very difficult. Is there an easier way?
 

Attachments

  • Screen Shot 2012-11-25 at 11.04.19 AM.png
    Screen Shot 2012-11-25 at 11.04.19 AM.png
    1.3 KB · Views: 455
Physics news on Phys.org
There is a much easier way. Try a substitution.
 
Haha, forgot about substituting.. clearly my calculus is rusty. Thanks!
 

Thread 'Finding the nth roots of a complex number'

There are two things I don't understand about this problem. First, when finding the nth root of a number, there should in theory be n solutions. However, the formula produces n+1 roots. Here is how. The first root is simply ##\left(r\right)^{\left(\frac{1}{n}\right)}##. Then you multiply this first root by n additional expressions given by the formula, as you go through k=0,1,...n-1. So you end up with n+1 roots, which cannot be correct. Let me illustrate what I mean. For this...
View full post »

Similar threads

Evaluate the definite integral in the given problem
Replies
1
Views
2K
Solving a linear differential equation with constant coefficients
Replies
9
Views
2K
Integration problem (algebraic+trigonometric function)
Replies
10
Views
1K
Integral of e^cosx: Answers Sought
Replies
11
Views
2K
Two ways of integration giving different results
Replies
9
Views
2K
Integrate 4cos(x/2)cos(x)sin(21x/2) Homework
Replies
2
Views
3K
Definite Integral of Product/Composite Function Given Graph
Replies
4
Views
2K
Proof that the definite integral of 1/ln(x) doesn't exist
Replies
7
Views
9K
Definite integral using only properties
Replies
7
Views
1K
Evaluate limit of this integral using positive summability kernels
Replies
2
Views
1K

Hot Threads

Recent Insights

Back
Top