Deflection and stress in a frame's vertical member

[parsec]

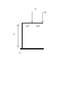
Please refer to the diagram attached.

I am trying to work out the peak stress and deflection of a vertical member in a simple steel frame.

I know that the vertical member will be subjected to a buckling stress, but I'm unsure as to whether the moment about O caused by the cantilevered forces F1 and F2 will result in an additional bending stress in the vertical member.

What is the peak stress in the vertical member (as a function of F1, F2, x, y and it's moment of area I)?

What is the peak deflection? Does it occur at the top of the vertical member due to a bending moment or is it near the center due to the first buckling mode?

Thanks in advance.

 

[Unrest]

What is the peak stress in the vertical member (as a function of F1, F2, x, y and it's moment of area I)?

The peak bending moment will be all along the vertical member. So the stress along that member will be constant except at the joints, where you can't really have any clue what the stress might be without more details there.

To find the stresses in the vertical member, find the compressive stress due to the vertical forces as if they were acting axially ( (F1+F2) / area ). Then find the stresses due to the bending moment (M = F1 * x/2 + F2 * x). Add/subtract them on the inner/outer surfaces.

What is the peak deflection? Does it occur at the top of the vertical member due to a bending moment or is it near the center due to the first buckling mode?

At the top. It won't buckle, at least not Euler buckling. That's because the offset load will cause it to deflect no matter how small the load, so it never gets the chance to reach an instability point.

 

[AlephZero]

It won't buckle, at least not Euler buckling. That's because the offset load will cause it to deflect no matter how small the load, so it never gets the chance to reach an instability point.

That is not necessarily true. If depends on the relative axial and bending stiffness of the vertical member.

In any case, the compressive load will reduce the bending stiffness and increase the lateral displacement even if it doesn't buckle. Look up the theory of beam-columns for the details.

 

[Unrest]

That is not necessarily true. If depends on the relative axial and bending stiffness of the vertical member.
[/quote
How? Sure if x is very small compared to the height, you may get something that looks like buckling because a small increase in load causes a large increase in deflection, but it won't have a discreet point at which it starts, like Euler buckling has. It'll just be general nonlinear elastic bahaviour.