Dependance of cut-in voltage of diode on scale of VI plot

[ShreyasR]

I have performed a small experiment to obtain the VI characteristics of a semiconductor diode using ANALOG DISCOVERY circuit design kit.

I have connected the arbitrary waveform generator (function generator) to a series combination of a 1N4007 diode and a 1 kilo ohm resistor.

To obtain the VI characteristics, I connected the terminals of oscilloscope channel 1 across the diode (to obtain the diode voltage as a function of time) and channel 2 terminals across the resistor. The voltage across the resistor is proportional to the current in the circuit according to ohm's law. (since I have chosen a 1 kΩ resistor, the numerical value of voltage (in volts) across R is the same as current (in milliamps)...

In XY mode, I obtained a plot channel 1 (V) vs channel 2 (I).

Then I changed the current scale of the VI plot by varying volts/division for channel 2.

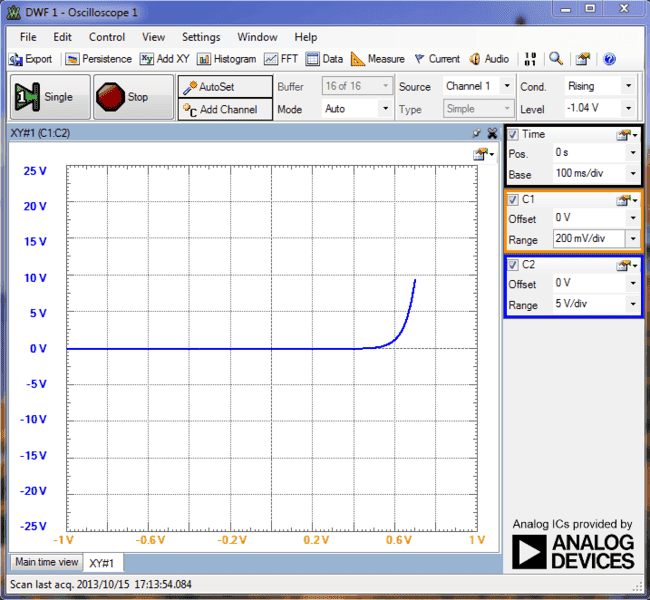
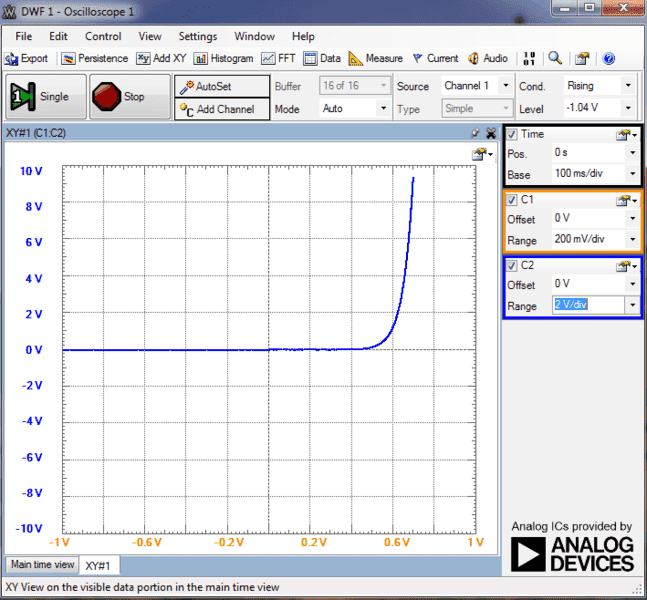
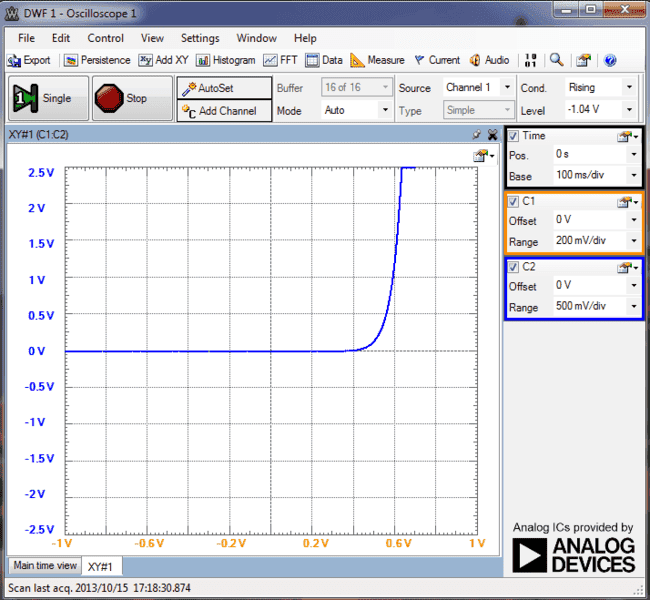
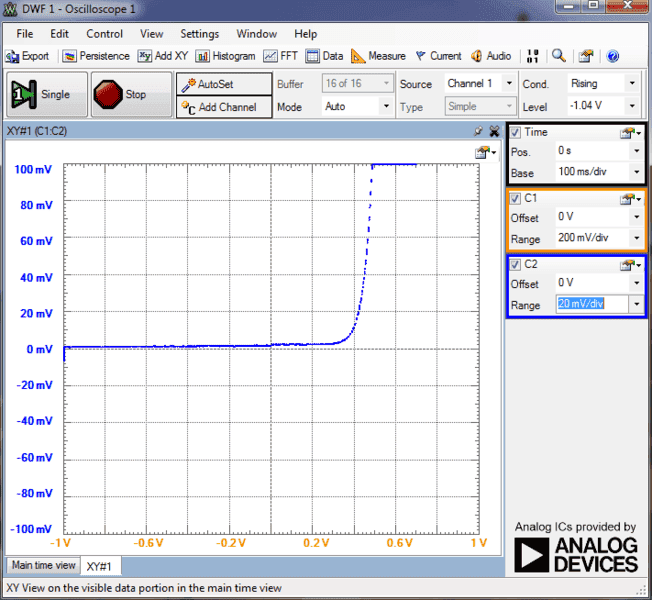
It appears to me that the cut in voltage of the diode is varying with the scale chosen. for 5V/div resistor voltage (5mA/div current), the knee voltage is about 6.5 V but as i decrease the scale, the knee shifts toward the left... For 20mV/div (20μA/div) the knee voltage is less than 0.4V. My inference to this observation is that the cut in voltage depends on the current range in which the diode is being operated in the circuit. Does this mean that for a silicon diode, the knee voltage need not be 0.6 to 0.7V? Or is that defined only for a particular current range? If i am using the diode as a rectifier, I might be dealing with currents as high as 2 to 3 amps. If i plot VI characteristics for that range, i believe the knee voltage will be more than 1V...

Why is it said that the knee voltage or cut in voltage of diode is 0.6 to 0.7 V?

Any detailed explanation about knee voltage of diode please reply! Thank you!

 

[mfb]

I think this is just an effect of the scaling. You can get a similar effect if you plot f(x)=e^x with different scales. Zooming in by a factor of e in vertical direction is equivalent to a shift of 1 in horizontal direction.

"Knee voltage" depends on the current range you consider, if the IV curve is exponential (or not so far away from that).
Can you set the scale to be logarithmic? ;)

 

[meBigGuy]

I think when you say you are varying the scale you are actually varying the current also. You are concerned with the actual voltage drop vs forward current that you are seeing. The forward current does vary significantly with forward current (how significantly depends on where on the curve you are) The diode equation expresses the relationship between forward current and voltage in terms of the reverse saturation current.

http://en.wikipedia.org/wiki/Diode

 

[ShreyasR]

I think when you say you are varying the scale you are actually varying the current also. You are concerned with the actual voltage drop vs forward current that you are seeing. The forward current does vary significantly with forward current (how significantly depends on where on the curve you are) The diode equation expresses the relationship between forward current and voltage in terms of the reverse saturation current.

http://en.wikipedia.org/wiki/Diode

No I am not actually varying the current. I used a triangular waveform with 10 V (peak to peak). the curve is obtained when the software generates the plot by capturing instantaneous voltage values across Diode and Resistor. If i am to relate this the the "manual" method of varying the supply voltage in regular steps and noting down the current values, what i am trying to say is that If I use a voltmeter and a milliammeter which can measure up to 3 or 4 decimal places, and if I tabulate V and I values for different ranges, and plot the graph for each range, (with appropriate range so as to accommodate the entire VI plot for that range) I get different knee voltages which can go as low as 0.35 V... If a choose a larger scale, the knee voltage can go upto 1 V. If this is the case, why is it said that the knee voltage is 0.2 to 0.3 volts for germanium diode and 0.6 to 0.7 for a silicon diode?

Also, when we take a look at the diode equation, We get a (very small) positive current value for any positive diode voltage. This contradicts the explanation: "The diode does not conduct until an external voltage of about 0.6 is applied so as to reduce the width of the depletion region/ provide the charge carriers with sufficient energy to cross the depletion region." I want a clear picture here to understand this properly.

 

[ShreyasR]

I think this is just an effect of the scaling. You can get a similar effect if you plot f(x)=e^x with different scales. Zooming in by a factor of e in vertical direction is equivalent to a shift of 1 in horizontal direction.

"Knee voltage" depends on the current range you consider, if the IV curve is exponential (or not so far away from that).
Can you set the scale to be logarithmic? ;)

Yes even I inferred that this is due to scaling effect... But this means if i am using the diode in nanoamperes range, may be the knee voltage will be about 0.2V. But that doesn't mean I am using a germanium diode does it? Isn't is important to mention the scale along with the knee voltage?

I guess there is an option to set the scale to be logarithmic. But never tried it! Well I will try it. But what should i expect when the scale is set to be logarithmic?

 

[meBigGuy]

I don't think the knee as visualized and judged on different scales is in any way meaningfull. Exponential curves will look self similar at any scale, as you can see.

There is conduction at small forward voltages as defined by the diode equation. The choice of 0.7V for silicon diodes is arbitrary but convienient. I suggest you work out values for Is and n and see if they fit.

Wikipedia says:

The third region is forward but small bias, where only a small forward current is conducted.

As the potential difference is increased above an arbitrarily defined "cut-in voltage" or "on-voltage" or "diode forward voltage drop (Vd)", the diode current becomes appreciable (the level of current considered "appreciable" and the value of cut-in voltage depends on the application), and the diode presents a very low resistance. The current–voltage curve is exponential. In a normal silicon diode at rated currents, the arbitrary cut-in voltage is defined as 0.6 to 0.7 volts. <snip> At higher currents the forward voltage drop of the diode increases. A drop of 1 V to 1.5 V is typical at full rated current

There is definitely conduction at low forward voltage, and your measurements show it. Anything said to the contrary is either wrong or being interpreted out of context.

 

[ShreyasR]

Thank you!

Anything said to the contrary is either wrong or being interpreted out of context.

I dint get that part... Can you please elaborate?

 

[mfb]

I'm not sure about diodes, but some bipolar transistors show a knee even in a logarithmic plot. This knee is scale-invariant. This could looks similar with diodes (and the base-emitter connection of a transistor is like a diode).

Every diode will have some leakage current (in both directions), but I don't know if your devices are sensitive enough to detect it (can be in the nA range or even below I think).

 

[meBigGuy]

There is definitely conduction at low forward voltage, and your measurements show it. Anything said to the contrary is either wrong or being interpreted out of context.

By this I was referring your your previous statement:

This contradicts the explanation: "The diode does not conduct until an external voltage of about 0.6 is applied so as to reduce the width of the depletion region/ provide the charge carriers with sufficient energy to cross the depletion region."

Feel free to ask more questions if you are not comfortable with any of what has been addressed.

 

[jim hardy]

just a quick thought here

the current through an ideal junction is given by the old standby formula
I= I₀e ^(qv/kt)

where
I₀= some very small current like 10^-11
v = voltage
q= charge of electron
k= Boltzmann constant( i think that's right name)
t=absolute temperature

A real diode of course has some series resistance because it's made of real material
so one would subtract from v that voltage drop

at very small currents the series resistance produces such small drop you can ignore it
but at high current it becomes significant

which is why power rectifiers have physically larger junctions than signal diodes, more area = less resistance

try some simple calculations from your observed data and see if you can figure out what is series resistance of that diode you tested
then repeat on a larger one

i'm away from home now with very limited internet access, so apologize for lack of a more thorough study of thread

good luck - old jim