Derivation of Carrier Concentration (ni)

m_keown2000
Messages
1
Reaction score
0
< Mentor Note -- thread moved to HH from the technical physics forums, so no HH Template is shown >[/color]

I am following a lecture on carrier concentration and I got to the point where the instructor said that for homework, derive the carrier concentration equation ni, which equals:https://www.physicsforums.com/attachments/81076

To derive ni you need to compute the following integral which I am having trouble solving:

Snapshot1.jpg


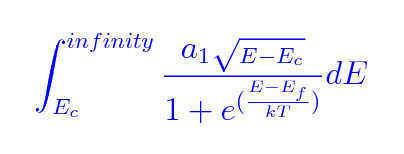
where:
Snapshot2.jpg


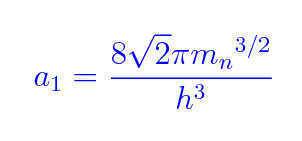
I tried Integration by parts and no luck. Any help would be greatly appreciated.
 

Attachments

  • Snapshot.jpg
    Snapshot.jpg
    7.2 KB · Views: 470
Last edited by a moderator:
Physics news on Phys.org
90make the variable change assume X = (E-[E][/C]/kT)
 

Thread 'Prove that the integral is equal to ##\pi^2/8##'

Prove $$\int\limits_0^{\sqrt2/4}\frac{1}{\sqrt{x-x^2}}\arcsin\sqrt{\frac{(x-1)\left(x-1+x\sqrt{9-16x}\right)}{1-2x}} \, \mathrm dx = \frac{\pi^2}{8}.$$ Let $$I = \int\limits_0^{\sqrt 2 / 4}\frac{1}{\sqrt{x-x^2}}\arcsin\sqrt{\frac{(x-1)\left(x-1+x\sqrt{9-16x}\right)}{1-2x}} \, \mathrm dx. \tag{1}$$ The representation integral of ##\arcsin## is $$\arcsin u = \int\limits_{0}^{1} \frac{\mathrm dt}{\sqrt{1-t^2}}, \qquad 0 \leqslant u \leqslant 1.$$ Plugging identity above into ##(1)## with ##u...
View full post »

Similar threads

What Steps Are Needed to Determine Coefficients in a Taylor Polynomial?
Replies
3
Views
1K
Determine dy/dx of the following and simplify if possible
Replies
11
Views
2K
Finding the Radius of Convergence for a Complex Function.
Replies
4
Views
2K
Introduction to Analysis by Bilodeau. Problem 1.3.3
Replies
18
Views
2K
Fourier series expansion problem
Replies
9
Views
3K
Tough Integration Problem Help
Replies
14
Views
2K
Proving eigenvalues and diagonalizability
Replies
29
Views
3K
Find the Fourier series for the periodic function
Replies
8
Views
2K
Work problem -- lifting water out of tanks
Replies
2
Views
2K
Taylor expanding a physics formula
Replies
18
Views
2K

Hot Threads

Recent Insights

Back
Top