fcoulomb
- 8
- 0
In my textbook there is an explanation of a derivation of D'Alembert equation for pressure waves. (##\frac{\partial^2 y}{\partial x^2}=\frac{\rho}{\beta}\frac{\partial^2 y}{\partial t^2}##)
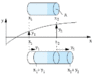
I put the picture (the only one I found on internet) but I'll call ##y_1 ,y_2## as ##\psi_1,\psi_2## and the second volume will be smaller that the first volume (unlike in the picture) so ##V_2<V_1##.
Starting by the fact that there is a pression on the left bigger than pressure on the right (so the volume will be smaller) ##P_1 >P_2##, I have ##(P_1-P_2)A=ma_x= \rho_0 A dx \frac{\partial^2 y}{\partial t^2}##.
Then I write ##P_{1,2}## as ##P_0+dP_{1,2}##, so ##dP_1-dP_2= -\frac{\partial(dP)}{\partial x} dx##.
Then I use the fact that ##dP=\beta \frac{d\rho}{\rho_0}## (with ##\beta## the coefficient of compressibility), but I need to write the ##d\rho## as a function of x, so
##\rho_0 V_1=(\rho_0+d\rho)V_2 \rightarrow \rho_0 A dx= (\rho_0+d\rho) A (dx-d\psi)##
Then by book says that I can write ##d\psi=\frac{\partial \psi}{\partial x}dx##, but I don't understand how these two variables are related.
Any help?
I put the picture (the only one I found on internet) but I'll call ##y_1 ,y_2## as ##\psi_1,\psi_2## and the second volume will be smaller that the first volume (unlike in the picture) so ##V_2<V_1##.
Starting by the fact that there is a pression on the left bigger than pressure on the right (so the volume will be smaller) ##P_1 >P_2##, I have ##(P_1-P_2)A=ma_x= \rho_0 A dx \frac{\partial^2 y}{\partial t^2}##.
Then I write ##P_{1,2}## as ##P_0+dP_{1,2}##, so ##dP_1-dP_2= -\frac{\partial(dP)}{\partial x} dx##.
Then I use the fact that ##dP=\beta \frac{d\rho}{\rho_0}## (with ##\beta## the coefficient of compressibility), but I need to write the ##d\rho## as a function of x, so
##\rho_0 V_1=(\rho_0+d\rho)V_2 \rightarrow \rho_0 A dx= (\rho_0+d\rho) A (dx-d\psi)##
Then by book says that I can write ##d\psi=\frac{\partial \psi}{\partial x}dx##, but I don't understand how these two variables are related.
Any help?