Deriving 1D Stress Field in a Bar

[Saladsamurai]

So in one of my classes, we very non-rigorously derived the 1D stress field for a bar with a longitudinal surface loading T(x) like show below:

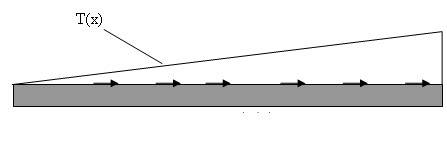
By taking out a differential element (assuming constant cross-sectional area) and applying good old Newton's Second, we end up with:

A \,d\sigma=-T(x)dx

which is easily separable to find \sigma(x).

My problem now is to do the same assuming that a concentrated loading is applied to one end like shown below:

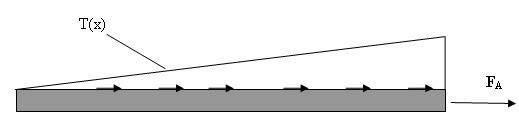
Now I feel like this should be simple in that we are only adding on a constant force. But I am not sure where to add it? That is, when I take out an arbitrary differential element, do I apply the F_A to the element? That is, do I assume that F_A acts along the entire length of the bar like in elementary statics? Like I have shown below:

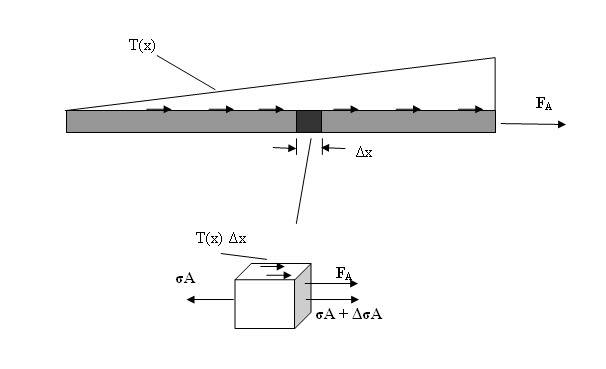
I ask because if I do this, I end up with the following differential EQ:

A \,\frac{d\sigma}{dx} = -T(x)-\frac{F_A}{dx}

which I am not sure what to do with (though I admit, I have not tried too hard).

Any insight would be appreciated.

~Casey

EDIT hmmm...maybe I am a little slow today I think that by multiplying through by dx might help out.

EDIT 2 maybe not...if I multiply through by 'dx' I end up with

d\sigma = -\frac{T(x)dx}{A} - \frac{F}{A}

which I cannot figure out how to integrate. The last term \frac{F}{A} does not have a 'differential' to which I would integrate with respect too.

As a matter of fact, it should act to remain as a constant stress; and it seems like it 'wants to' but I cannot get the mathematics to show it.

 

[Brian_C]

Have you learned anything about Airy Stress Functions? I'm pretty sure this can be solved using an appropriate combination of stress functions.

Also, how is the bar being supported? The object in your figure is not in static equilibrium.

 

[Saladsamurai]

Have you learned anything about Airy Stress Functions? I'm pretty sure this can be solved using an appropriate combination of stress functions.

Also, how is the bar being supported? The object in your figure is not in static equilibrium.

Hi Brian,

It's cantilevered. No, I have not learned about the Airy stress functions. But, I feel like this should be pretty cut and dry Newton's Law here. I just think that something is going wrong with my assumption that I can put F_A in with the other differential forces. I thought that I could do this using the principle of transmissibility , but perhaps this is an improper application of the principle.

I think that it might be better to include F_A as a boundary condition.

 

[Brian_C]

See the attached pdf file. If the surface traction is constant, the normal stress will increase linearly with distance from the end of the bar.

The Airy stress function approach is appropriate if you want a more rigorous solution.

 

[Mapes]

As a matter of fact, it should act to remain as a constant stress; and it seems like it 'wants to' but I cannot get the mathematics to show it.

Agreed. Try drawing your first differential element at the location where the point force acts; you'll find that you have to add an equal and opposite force on the right side of the element to keep the element from translating. Any differential element to the left of the right end must therefore also include this force. Does this help?

 

[vargasjc]

Are you taking into consideration the deflection of the bar due to the T(x) load?