Deriving the equation for magnetic induction

[raul_l]

Homework Statement

We have a straight wire with radius R. What is the magnetic induction through point A at a distance of r?
In other words, derive the equation $$B=\frac{\mu_{0}i}{2\pi r}$$ by using $$d\vec{B}=\frac{\mu_{0}i}{4\pi r^2}(d\vec{l} \times \vec{u_{r}})$$

Homework Equations

$$d\vec{B}=\frac{\mu_{0}i}{4\pi r^2}(d\vec{l} \times \vec{u_{r}})$$

The Attempt at a Solution

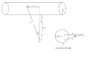
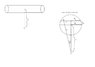
Now, I know there are a couple of methods for doing this, some of them being quite simple. But I'm specifically interested in solving the problem by using just one equation (the Biot-Savart law) and integrating it over the entire volume of the wire (assuming we have an infinitely long straight wire with constant radius and density). I guess this means bringing in a triple integral. As far as I know $$dB=\frac{\mu_{0}i}{4\pi s^2}\cos{\alpha}dl$$ where $$\cos{\alpha}=\frac{r}{s}$$ (see drawing1) in which case we are dealing with an infinitely thin wire and it would be not too difficult to solve $$B=\int^{\infty}_{-\infty} \frac{\mu_{0}i}{4\pi s^2}\cos{\alpha}dl$$. However, assuming that we have a real wire with a radius R, we need one more angle to describe the position of dl with respect to point A. (see drawing2). If any of this makes any sense at all, I should get $$dB=\frac{\mu_{0}i}{4\pi x^2}\cos{\alpha}\cos{\phi}dl$$ where $$\cos{\alpha}=\frac{a}{s}$$, $$\cos{\phi}=\frac{s}{x}$$ and r is the distance between point A and the center of the wire. I haven't learned yet how to create triple integrals (only double integrals so far) so this is why it's a little bit beyond my level. Any thoughts on how to continue? Am I even moving in the right direction here?

 

[jhicks]

Be careful in choosing your differential elements. As it stands right now, yours doesn't make too much sense because you ultimately wish to integrate over a volume $$V$$ containing a constant current density $$\vec{J}$$.

Use the form $$d\vec{B} = \frac{\mu_0}{4 \pi r^2} (\vec{J}dV \times \vec{r})$$ to start with. By forgoing the use of vector calculus, however, setting up the integrals properly may be pretty difficult. For example, the bounds of $$\phi$$ over which to integrate are not nearly as simple as $$\alpha$$. As to the solution, you may not be able to find an exact result I'm afraid. I have done a few similar calculations and I ended up computing them in MATLAB.

 

[raul_l]

Interesting. I guess that makes sense. I was wondering about this however. Is it right for me to assume that the bounds of $$\phi$$ are functions of $$\alpha$$ and a?

 

[raul_l]

I finally figured it out. I'm going to divide the wire into infinitely thin planes, each plane perpendicular to r (the distance between point A and the center of the wire). Each plane I will divide into infinitely thin straight lines, so as if the whole wire represents a bundle of infinitely thin straight "wires" (see wire.jpg, where each line represents a single point on the cross-section of the wire). Each of those lines has a current di running through them inducing a magnetic field vector $$d\vec{B}$$ at point A. All I have to do is find a way to express the sum of all the modules of $$d\vec{B}$$ created by each line to get the answer I'm looking for.

symbol definitions:
r - distance between point A and the center of the wire
h - distance between the observable plane and the center of the wire (r+h is the distance between point A and the observable plane)
R - radius of the wire
R' - half the width of the observable plane. It depends on the value of h, therefore R'(h).
x - distance between line B (in the drawing it appears as point B) and the central line of the observable plane
s - distance between line B and point A
phi - angle between r and s (see drawing)

First, I will observe the magnetic induction created at point A by the central line of the wire. It's easy to show that that would be $$dB=\frac{\mu_{0}di}{2\pi r}$$. For any other line I would have to substitute r with s (distance between the observable line and point A). For example for line B I get $$dB=\frac{\mu_{0}di}{2\pi s}\cos{\phi}=\frac{\mu_{0}jdS}{2\pi s}\frac{r+h}{s}=\frac{\mu_{0}j(r+h)dxdh}{2\pi s^2}=\frac{\mu_{0}j(r+h)dxdh}{2\pi ((r+h)^2+x^2)}$$
By integrating it over x from -R' to R' I get the magnetic induction at point A induced by each plane. To find the sum of all planes I have to integrate it over h from -R to R. $$B=\int^{R}_{-R}{\int^{R'(h)}_{-R(h)}{\frac{\mu_{0}j(r+h)}{2\pi ((r+h)^2+x^2)}dx}dh}=\int^{R}_{-R}{2\int^{R'(h)}_{0}{\frac{\mu_{0}j(r+h)}{2\pi ((r+h)^2+x^2)}dx}dh}=\int^{R}_{-R}{\int^{R'(h)}_{0}{\frac{\mu_{0}j(r+h)}{\pi ((r+h)^2+x^2)}dx}dh}$$

$$h^2+R'^2=R^2 \Rightarrow R'(h)=\sqrt{R^2-h^2}$$
Also, I want to keep the current constant, independent of the radius of the wire, therefore I will substitute $$j=\frac{i}{4\pi R^2}$$ to get $$B(r,R,i)=\int^{R}_{-R}{\int^{R'(h)}_{0}{\frac{\mu_{0}\frac{i}{4\pi R^2}(r+h)}{\pi ((r+h)^2+x^2)}dx}dh}=\int^{R}_{-R}{\int^{R'(h)}_{0}{\frac{\mu_{0}i(r+h)}{4R^2 ((r+h)^2+x^2)}dx}dh}$$ which gives me the magnetic induction of an infinitely long straight wire with the radius R at point A. So far I haven't found a computer program that could solve this kind of integral but by using different values of r, R and i to numerically find B(r,R,i) I believe that I can safely conclude that
$$B(r,R,i)=\int^{R}_{-R}{\int^{R'(h)}_{0}{\frac{\mu_{0}i(r+h)}{4R^2 ((r+h)^2+x^2)}dx}dh}=\left\{\begin{array}{cc}\frac{\mu_{0}ir}{2\pi R^2},&\mbox{ if } r<R \\\frac{\mu_{0}i}{2\pi r}, & \mbox{ if } r \geq R\end{array}\right.$$