Brute
- 8
- 0
Homework Statement
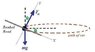
Derive the formula to calculate the angle at which the road should be banked to prevent the car from skidding(Ignore force of friction).
Homework Equations
tan x = v^2/gr ----- answer
mv^2/r = fc
The Attempt at a Solution
I get how they derived the formula due to this website http://batesvilleinschools.com/physics/phynet/mechanics/circular%20motion/banked_no_friction.htm
My question is how can I do it, by putting mg in terms of horizontal and vertical components, instead of Fn.(I know the website explains why it makes more sense to do it that way, but I still want to know).
My attempt:
Forces in Y = 0:
Fn - mg cos x = 0
Fn = mg cos x
Forces in X:
mg sin x = mv^2/r
g sin x = v^2/r
sin x = v^2 / gr --stuck not the same answer
If someone can please explain what I am doing wrong much help appreciated.
Last edited by a moderator: