Designing a Stable Crane: Finding Reactions & Max Load

Click For Summary
SUMMARY

The discussion focuses on designing a stable crane by calculating the reactions at the jib and determining the maximum load it can lift. The user established that the maximum weight the crane can handle is 600 kg, translating to a force of 6000 N. The calculations involve ensuring that the sum of all forces equals zero and that the moments at the base of the vertical beam are balanced. The user seeks to confirm the stability of the crane under these conditions and the reactions at the intersection of the horizontal and vertical beams.

PREREQUISITES
  • Understanding of static equilibrium in mechanics
  • Knowledge of crane design principles
  • Familiarity with force and moment calculations
  • Basic concepts of pulley systems
NEXT STEPS
  • Research static equilibrium principles in mechanical systems
  • Study crane stability analysis techniques
  • Learn about calculating moments in structural engineering
  • Explore pulley system mechanics and load distribution
USEFUL FOR

Mechanical engineers, civil engineers, and students involved in structural design and stability analysis of cranes and lifting systems.

dreistein
Messages
3
Reaction score
0

Homework Statement


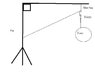
I'm to design a crane, and therefore I need to find the reactions in the jib and also make the crane stable.
1. I need to find the max. load that the crane is able to lift. Therefore i have to find the reactions where the horisontal and vertical boom is meeting.
2. I need to find out the moment in the bottom of the vertical beam in order to make the crane stable. Now i should have the max weight, and therefore the weight of the stone. And it should be easier to calculate


Homework Equations





The Attempt at a Solution


The sum of all the forces needs to be 0. F=0
The angle is 90 degrees, so that is not going to be a problem
The wire from the horisontal beam is only ½ m.
But since i don't know the weight of the stone, I don't know where to begin?
 

Attachments

  • Physics.JPG
    Physics.JPG
    9.5 KB · Views: 528
Physics news on Phys.org
as I'm using a pulley system i found out that my weight max is going to be 600 kg, but is my crane able to do this? What will the reactions be where they meet each other? And will they be able to lift this?
 
I assume that the reaction would be: moment = 0, 6000N*3m-R*3m=0
Therefore Reaction where the beams are meeting would be 6000N
 

Thread 'Magnitude of buoyant force in fluids of different densities'

The book claims the answer is that all the magnitudes are the same because "the gravitational force on the penguin is the same". I'm having trouble understanding this. I thought the buoyant force was equal to the weight of the fluid displaced. Weight depends on mass which depends on density. Therefore, due to the differing densities the buoyant force will be different in each case? Is this incorrect?
View full post »

Similar threads

Tower Crane Forces: Find the Mass of Counterweight
  • · Replies 13 ·
Replies
13
Views
6K
Lifting a 30m 35te Spud Leg: Crane Weight Calculation
  • · Replies 8 ·
Replies
8
Views
2K
Finding the WORK done by a crane in lifting a load
  • · Replies 14 ·
Replies
14
Views
8K
Project to design and calculate the hydraulics for a deck crane
  • · Replies 2 ·
Replies
2
Views
2K
Positioning a Counterweight for Heavy Crane Lifting
  • · Replies 3 ·
Replies
3
Views
5K
Calculating maximum load and counterweight of a tower crane
  • · Replies 3 ·
Replies
3
Views
19K
Raising a farm windmill tower
  • · Replies 5 ·
Replies
5
Views
2K
Given force, need to determine what bearing to use for a crane
  • · Replies 69 ·
3
Replies
69
Views
5K
Calculate Torque in 12.2m Crane - 18kN Load, 67kN Tension
  • · Replies 5 ·
Replies
5
Views
17K
To what extent does this system behave as a pendulum?
  • · Replies 1 ·
Replies
1
Views
1K