Vishera
- 72
- 1
Homework Statement
Homework Equations
The Attempt at a Solution
Here is my attempt: http://i.imgur.com/oKjwI8O.png
The problem is at the end, I get 0=0. What did I do wrong?
Vishera said:Homework Statement
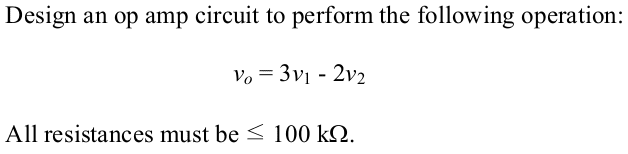
Homework Equations
The Attempt at a Solution
Here is my attempt: http://i.imgur.com/oKjwI8O.png
The problem is at the end, I get 0=0. What did I do wrong?
berkeman said:Can you post a drawing of your opamp circuit, with the resistor names labeled? Thanks.
rude man said:You sure it isn't Vo = 3V2 - 2V1?
rude man said:You sure it isn't Vo = 3V2 - 2V1?
Vishera said:Is there any specific reason why you can't the following equation to:

to:
vo=3v1-2v2?
I understand that I get 0=0 but why do I get 0=0? Algebraically speaking, why would it matter if it were vo = 3v2 - 2v1 or vo=3v1-2v2?
donpacino said:combing your two equations the way you initially had them -R2/R1 would have to equal three.
that would imply that you have a negative resistance, which is impossible