rasgar
- 32
- 0
need help on potential energy problem (less than 45 min left))
This is due online at 11:00 pm tonight! Otherwise I wouldn't post here I'd ask my prof for help.
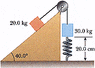
A 20.0 kg block is connected to a 30.0 kg block by a string that passes over a light, frictionless pulley. The 30.0 kg block is connected to a spring that has negligible mass and a force constant of 280 N/m, as shown in the figure below. The spring is unstretched when the system is as shown in the figure, and the incline is frictionless. The 20.0 kg block is pulled 20.0 cm down the incline (so that the 30.0 kg block is 40.0 cm above the floor) and released from rest. Find the speed of each block when the 30.0 kg block is 20.0 cm above the floor (that is, when the spring is unstretched). P.S. the incline is 40 degrees above the horizontal and the 20kg weight is on that horizontal, while the 30kg block is vertical.
.5mV^2=PE
.5Kx^2=PE
KE=PE
I set up the problem to have potential energy of the 30kg block increased and the 20kg block decreased, with the potential energy in the spring increased. This came out to 30*9.81*.2-20*9.81*.2/sin(40)+.5*280*.2^2. With the total potential energy of the system I promptly set it equal to the kinetic energy and solved for the mass of the system (sqrt(2*PE/50)). The answer was not correct. I looked in my textbook for a similar question and found one exactly like it, except with the spring constant being 250. The back of the book said the answer was 1.24m/s. I tried to replicate the results with my previous attempt with no avail. And I've tried all deviations, such as changing the plus and minuses, and solving for individual masses. Got close but no cigar. The book and online homework said specifically to carry out all operations to 4 decimal places, and I did, so that's not the problem either. For the love of god help me quickly.
This is due online at 11:00 pm tonight! Otherwise I wouldn't post here I'd ask my prof for help.
Homework Statement
A 20.0 kg block is connected to a 30.0 kg block by a string that passes over a light, frictionless pulley. The 30.0 kg block is connected to a spring that has negligible mass and a force constant of 280 N/m, as shown in the figure below. The spring is unstretched when the system is as shown in the figure, and the incline is frictionless. The 20.0 kg block is pulled 20.0 cm down the incline (so that the 30.0 kg block is 40.0 cm above the floor) and released from rest. Find the speed of each block when the 30.0 kg block is 20.0 cm above the floor (that is, when the spring is unstretched). P.S. the incline is 40 degrees above the horizontal and the 20kg weight is on that horizontal, while the 30kg block is vertical.
Homework Equations
.5mV^2=PE
.5Kx^2=PE
KE=PE
The Attempt at a Solution
I set up the problem to have potential energy of the 30kg block increased and the 20kg block decreased, with the potential energy in the spring increased. This came out to 30*9.81*.2-20*9.81*.2/sin(40)+.5*280*.2^2. With the total potential energy of the system I promptly set it equal to the kinetic energy and solved for the mass of the system (sqrt(2*PE/50)). The answer was not correct. I looked in my textbook for a similar question and found one exactly like it, except with the spring constant being 250. The back of the book said the answer was 1.24m/s. I tried to replicate the results with my previous attempt with no avail. And I've tried all deviations, such as changing the plus and minuses, and solving for individual masses. Got close but no cigar. The book and online homework said specifically to carry out all operations to 4 decimal places, and I did, so that's not the problem either. For the love of god help me quickly.
Last edited: