MiMiCiCi22
- 4
- 0
Homework Statement
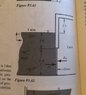
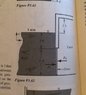
Determine the total force and its direction (left or right) due to water and air pressure in the surface shown in Fig. P3.62 (lb f). The door is hinged at the top and is 6 feet wide. See attached image.
Homework Equations
Fp (force of pressure) = specific weight of fluid * depth to center of gravity * Area
P=F/A
Pg (gauge pressure) = specific weight of fluid * depth
Specific weight of water = 62.4 lb/ft^2
lbf = pounds of force
The Attempt at a Solution
I first tried to find the force of pressure from the water acting on the side of the door...
Fp = (62.4 lbf/ft^2)*(3ft+2.5ft)*(5ft)*(6ft)
Fp = 10296 lbf
I then thought that if I added the force of pressure from the water acting on the side of the door to the force of pressure from the air acting on the side of the door, I would be able to find the total force. I first converted 2 atm to lbf/ft^2...
2 atm * (0.0209 lb/ft^3)/(9.869x10^-3 atm) = 4235.48 lbf/ft^2
I then tried to find force using this pressure...
F = PA = (4235.48 lbf/ft^2)*(5ft)*(6ft)
At this point, my professor told me that I was solving it wrong.