Fronzbot
- 58
- 0
NOTE- Images are thumbnails, click to enlarge
Show that the positive feedback gain expression for the circuit below is
v2/v0 = 1/[3 + j(wL/R - R/WL)]
(anything in red I added to the original problem)
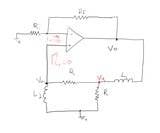
(above)
Along with the below calculations, I also attempted to combine the components but that didn't work either. I combined R and L2 in series, those in parallel with the other R and then in series with L1 (let's call all of that Zt). I then said (V2-V0)/Zt = 0 and proceeded to solve for V2/V0 but did not get the right answer. I thought that that should work since this is an ideal op-amp and no current is flowing between L2 and R, but alas I did not get the correct answer. Any guidance?

Homework Statement
Show that the positive feedback gain expression for the circuit below is
v2/v0 = 1/[3 + j(wL/R - R/WL)]
(anything in red I added to the original problem)
Homework Equations
(above)
The Attempt at a Solution
Along with the below calculations, I also attempted to combine the components but that didn't work either. I combined R and L2 in series, those in parallel with the other R and then in series with L1 (let's call all of that Zt). I then said (V2-V0)/Zt = 0 and proceeded to solve for V2/V0 but did not get the right answer. I thought that that should work since this is an ideal op-amp and no current is flowing between L2 and R, but alas I did not get the correct answer. Any guidance?