chwala
Gold Member
- 2,827
- 415
- Homework Statement
- Determine the type of correlation that exists between the two given variables.
- Relevant Equations
- Pearson's correlation coefficient
Kindly see the attached problem below (i find the topic to be easy and straightforward). My concern is only on the highlighted part:
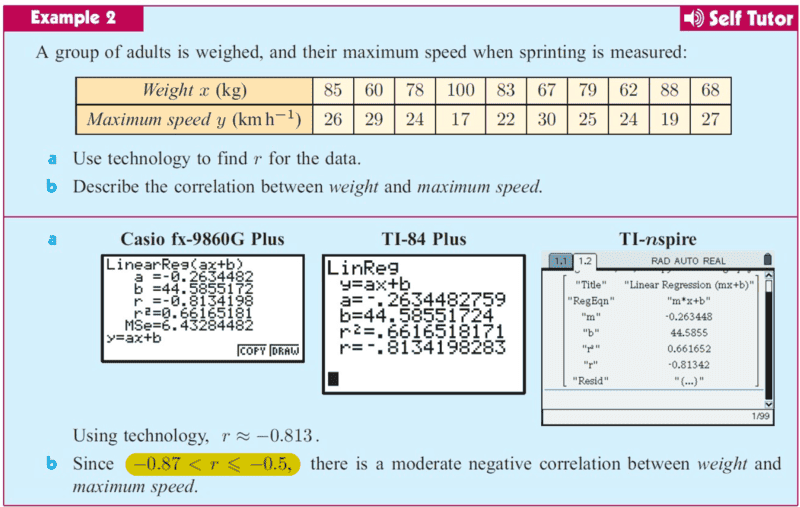
In my understanding, to define the type of correlation i have always approached a straightforward approach.
For value ##1## perfect positive correlation and value ##-1## perfect negative correlation.
any value between ##0.5-1## strong positive correlation.
any value between ##0-0.5## weak positive correlation.
any value between ##-0.5-0## weak negative correlation and so on...
In addition, i have always considered values ##0.5## and ##-0.5## as either positive/weak.
Is my approach correct?
Now to my question, how did they arrive at the interval on the highlighted part above (in yellow). Kindly see table below as a reference...how did they arrive at the values indicated on the table? or they used some data and then went ahead to see how the data is spread out on the graph (by considering outliers where necessary) ...then used Pearson's correlation coefficient to come up with some deduction...i think that's how they did it.
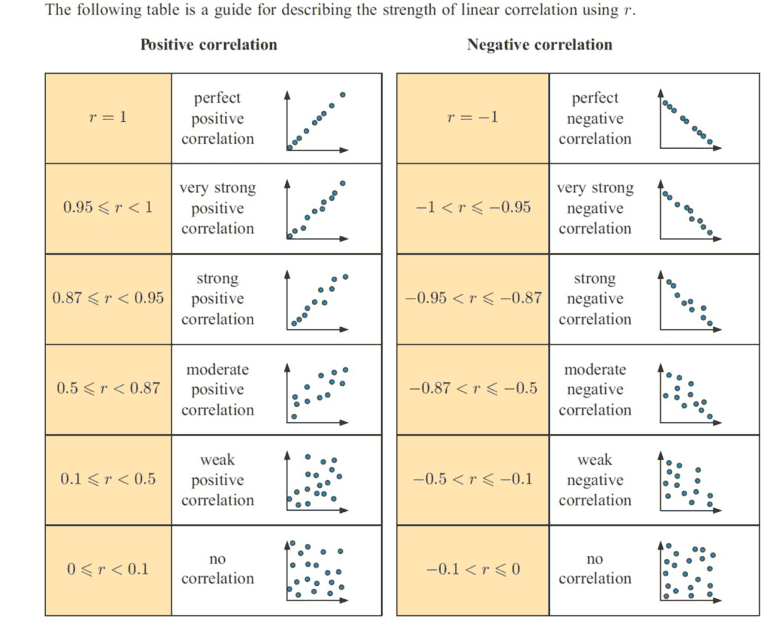
In my understanding, to define the type of correlation i have always approached a straightforward approach.
For value ##1## perfect positive correlation and value ##-1## perfect negative correlation.
any value between ##0.5-1## strong positive correlation.
any value between ##0-0.5## weak positive correlation.
any value between ##-0.5-0## weak negative correlation and so on...
In addition, i have always considered values ##0.5## and ##-0.5## as either positive/weak.
Is my approach correct?
Now to my question, how did they arrive at the interval on the highlighted part above (in yellow). Kindly see table below as a reference...how did they arrive at the values indicated on the table? or they used some data and then went ahead to see how the data is spread out on the graph (by considering outliers where necessary) ...then used Pearson's correlation coefficient to come up with some deduction...i think that's how they did it.
Last edited: