Determing unknown weight of an hanging object in a systen

[GoGoGadget]

Homework Statement

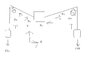
1. You have been asked to test a new device for measuring the weight of tissue samples. The device
consists of two light wires attached at one end to a support. A small container is attached to the other
end of each wire. Initially each container hangs straight down. The wires are far enough apart so the
containers hanging on them don’t touch. One of the containers has a very accurately known weight
while the other contains the sample whose weight you wish to determine. A power supply is slowly
turned on so that electromagnets in each container cause them to slowly move away from each other.
When the power supply is kept at its operating value, the containers stay at the same horizontal level.
At that point, each of the wires supporting them makes a different angle with the vertical and that angle
is measured. To test the device, you calculate the weight of one container and its contents from the
measured angles and the known weight of the other container. You will then check your calculation in
the laboratory using a variety of different objects as samples.

Homework Equations

F = ma

w = mg

The Attempt at a Solution

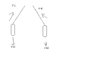
Below are my attached picture and diagram of the system. In the first picture, I drew what the system looked like in equilibrium. In the second picture, I show the changes in the system when the angles are present when the wires are stretched out vertically. What I have so far:

Variables:

Fs = Force of stopper

Fw = Force of wire

FE1 = Force of Earth on container 1

FE2 = Force of Earth on container 2

Equations:

F_x = F_w - F_s Cos θ = 0


F_y = F_w - F _E1 Sin θ

F _y = F_w - F_E2 Sin θ

From my understanding of this problem, I believe I need to find the weight of container 1, where the F = E1. And I know we do know the weight of container 2, E2. But from here, I have no idea how to go about setting the equations to be equal to one another or how to connect the two containers together into one equation. Any help is greatly appreciated.

 

[haruspex]

I'm not sure about your diagrams. What's the block in the middle? As I read the question, each wire is on its own support. Since, with the power on, the wires hang at different angles yet the containers are at the same horizontal level, I would assume either the supports are at different heights or the wires are of different lengths (or both). I've a suspicion they haven't told you quite enough.
In your equations, you have one for each weight, yet you have the same symbols Fy, Fw and theta in each. That's confusing, since each each of them can be different.
And what exactly do your Fx and Fy stand for? If they're net horizontal and vertical forces then your equations are quite wrong.

 

[GoGoGadget]

I'm not sure about your diagrams. What's the block in the middle? As I read the question, each wire is on its own support. Since, with the power on, the wires hang at different angles yet the containers are at the same horizontal level, I would assume either the supports are at different heights or the wires are of different lengths (or both). I've a suspicion they haven't told you quite enough.
In your equations, you have one for each weight, yet you have the same symbols Fy, Fw and theta in each. That's confusing, since each each of them can be different.
And what exactly do your Fx and Fy stand for? If they're net horizontal and vertical forces then your equations are quite wrong.

In my original equation, I think I had misunderstood the problem and drew the diagram to show the wires hanging from the same stopper, which the block was supposed to represent. I've redrawn the problem in the attachments below. The only I wasn't sure of was how to show the angles that are represented. I drew the system, show it in equilibrium and then with the wires hanging so they can potentially form an angle. However, I didn't show my angles in my second diagram as I was not sure how I can show them without drawing in extra variables that aren't there. However, I know that vectors could be shown too for the sides of the potential triangles that each wire makes. FW1 could shown FW1_x and FW1_y on the wire hanging on the left and then FW2 could be shown with FW2_x and FW2_y on the right. And Fx and Fy were supposed to show the sum of forces in either direction. So potentially now, I'm thinking:

F_x: FW2 sin θ₂ + FW1 sin θ ₁ = 0

F_y: FW2 cos θ₂ - E1 +FW1 sin θ₁ - E2 = 0

I'm not sure if I'm thinking about this correctly or not. Any further input is great. Thanks a lot!

 

[haruspex]

F_x: FW2 sin θ₂ + FW1 sin θ ₁ = 0

If you're measuring both angles in the same direction (so one will be negative) then yes.

F_y: FW2 cos θ₂ - E1 +FW1 sin θ₁ - E2 = 0

There is no relationship between the vertical forces on one and the vertical forces on the other. That should be two separate equations.