Determining Current Magnitude & Direction for Stationary Bar on Inclined Plane

[arierreF]

Homework Statement

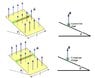
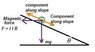
A conducting bar of length is placed on a frictionless inclined plane which is tilted at
an angle θ from the horizontal, as shown in annexed figure.

A uniform magnetic field is applied in the vertical direction. To prevent the bar from
sliding down, a voltage source is connected to the ends of the bar with current flowing
through. Determine the magnitude and the direction of the current such that the bar will
remain stationary.

Homework Equations

\vec{F_{B}} = q\ \vec{v}\times \vec{B}
\vec{F_{B}} = i\ \vec{l}\times \vec{B}

The Attempt at a Solution

The magnitude i think it is obvious.

The gravitational force action on particle is:

F = mg sin\theta

So in order to cancel this force, the magnitude of magnetic force is:

|F_{B}| = mg sin\thetaThe magnitude of the current is:

|i| = \frac{mg sin\theta }{l B sin 90 -\theta }My problem is too find the direction of the current mathematically. I can easily know it by applying the right hand rule.

Any tip for getting the current direction?

 

[TSny]

Hi, arierreF

The gravitational force action on particle is:

F = mg sin\theta

To be nitpicky: the magnitude of the gravitational force is mg. What you wrote down is the magnitude of the component of the force that acts parallel to the plane. [EDIT: And instead of "particle" I think you meant "rod"]

So in order to cancel this force, the magnitude of magnetic force is:

|F_{B}| = mg sin\theta

Again, this will be the component of the magnetic force that acts parallel to the plane. It is not the magnitude of the magnetic force itself.

The magnitude of the current is:

|i| = \frac{mg sin\theta }{l B sin 90 -\theta }

This is not correct because of the comments above. [Edit: Actually, I think this is the correct answer. But I'm not sure if your logic is correct. (Maybe it is.)]

My problem is too find the direction of the current mathematically. I can easily know it by applying the right hand rule.

Any tip for getting the current direction?

Yes, you are going to need to find the direction of the magnetic force in order to determine its component along the plane. Can you tell us your understanding of how to use the right hand rule?
[EDIT: I don't really understand why you need to find the direction of the current "mathematically". The best way is just to use the right hand rule.]

 

[arierreF]

With the right hand rule, we can know the direction of the magnetic force (thumb). The fingers represent the velocity and the magnetic field.

So knowing that the magnetic field is pointing up \hat{k} , the magnetic force is pointing to the left with a certain angle \hat{k} - \hat{j} . Then the velocity, or the direction of the current is \hat{i}.

(charge is positive)About the forces.

Fg_{paralel to plane} =mg sin \theta
Fg_{perpendicular to plane} is canceled by normal reaction of the plane

F_{b} = i\vec{l}\times\vec{B}

because the angle between l and B is (90 - \theta) º , then F_{b} = ilB sin (90- \theta )º = ilBcos \theta
The answer to the magnitude of the current is

i = \frac{mg}{lB} ??

 

[TSny]

We need to be clear on the direction of the magnetic force. The current in the bar can only flow in one of two directions as shown in the attachment. For each case, in what direction is the magnetic force? Which of those two cases do you need in order to prevent the rod from sliding down the slope?

 

[arierreF]

if the current is into page then the magnetic force is going to point to the right.
if out of page then is going to point to the left.

So in order to prevent the rod from sliding down the stop, the current must has the direction out to the page.

 

[TSny]

Correct. What is the magnitude of the total magnetic force pointing to the left when the current is out of the page?

 

[arierreF]

\vec{F}= i\vec{l}\times\vec{B}

the direction of l makes a angle (90- θ) with the direction of B

So

F = i{l}{B}sin(90 -\theta)

 

[TSny]

No. When doing the cross product of two vectors, you need to use the angle between the two vectors. What is the angle between $\vec{l}$ and $\vec{B}$?

 

[arierreF]

No. When doing the cross product of two vectors, you need to use the angle between the two vectors. What is the angle between $\vec{l}$ and $\vec{B}$?

maybe that's where i am getting the error.EDIT: \vec{B} makes a (pi/2 - (θ)) angles with \vec{l}

 

[TSny]

\vec{B} is vertical while \vec{l} is horizontal. So, what is the angle between them? [Edit: Remember, \vec{l} points in the same direction as the current.]

 

[arierreF]

damn, it is 90 degrees. Seeing it from your attached image.

 

[TSny]

Right! So what's the magnitude of the magnetic force?

 

[arierreF]

Right! So what's the magnitude of the magnetic force?

So

{F} = ilB

magnitude of i
i = \frac {mg sin \theta}{lB}

 

[TSny]

Correct for total magnetic force, but not for the current. You've still got some vector components to deal with. It's the components of the forces along the slope that need to balance. See attachment.

 

[arierreF]

The component along slop that is pointing is responsible of make the rod to slid down is:

mg sin (\theta)

The component along slop that is pointing is responsible of preventing the rod to slid down is:

ilBcos (\theta)

Right? So to the rod stay stationary, ilBcos (\theta) = mg sin (\theta)

 

[TSny]

Yes. Good.

 

[arierreF]

so to finalize, i = \frac{mg}{lB} tg \theta

 

[TSny]

Yes, that gets it. (Same answer as you originally proposed! But hopefully the solution is clear now.)

 

[arierreF]

Yes, that gets it. (Same answer as you originally proposed!. But hopefully the solution is clear now.)

Yes, much clear!

Thanks a lot for your time!