Differential Equation for a Wien Bridge Oscillator

[d.arbitman]

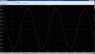
I am trying to write out a differential equation for the Wien bridge oscillator circuit. I have attached a picture of the circuit. I am considering ideal conditions. I am trying to solve for the output voltage but I need help setting up the differential equation.

 

[d.arbitman]

I went through this a couple of times and still haven't arrived at a right answer.


I attached my differential equation, some initial conditions and the plot of the solution. However, the solution EXPLODES. Now I'm stuck. By the way, I used the component values from the circuit shown in the picture in my first post.

 

[The Electrician]

This is exactly what an oscillator should do. In a real oscillator, you will need a non-linear element to reduce the gain when the oscillations reach a particular amplitude. Search the web for Wien Bridge oscillator and you will find discussion of various methods to achieve this.

 

[d.arbitman]

This is exactly what an oscillator should do. In a real oscillator, you will need a non-linear element to reduce the gain when the oscillations reach a particular amplitude. Search the web for Wien Bridge oscillator and you will find discussion of various methods to achieve this.

Bill Hewlett used a lamp to decrease the gain as the output increased. That's not exactly my problem. I have attached a picture of the output from an LTspice simulation. You can see that it oscillates with an amplitude of about 420mV. My simulation has two problems. It grows extremely quickly and its frequency is incorrect. I have verified that the frequency is incorrect by using Mathematica to solve the equation that I derived symbolically. The frequency was way too high. This suggests that I did not set up the differential equation correctly.

I just need help in setting up a differential equation assuming ideal components.

 

[The Electrician]

Your LTspice schematic shows V1 and V2, but your differential equation uses V(t). How does your differential equation correspond to some node on the schematic? Which node?

Why is the amplitude in your simulation not increasing without bound? What limits the amplitude?

 

[d.arbitman]

It's the output of the op amp.

 

[The Electrician]

The period of oscillation in your LT spice simulation appears to be about 65 mS; similarly in the image of post #2. This corresponds to a frequency of about 15 Hz.

The frequency of oscillation for a Wien bridge oscillator is given by 1/(2 Pi R C):

http://en.wikipedia.org/wiki/Wien_bridge_oscillator

Your component values give a frequency of 15.9 Hz.

All three are consistent. I don't see what the problem is.

Does the image in post #2 show the result of a numerical solution to the diffeq? Is the problem that your symbolic solution is not giving the same frequency?

 

[d.arbitman]

The image (w/a white background) in post #2 is the numerical solution using the built-in numerical ODE solver. I can't recall what the frequency was in the symbolic solution, BUT it wasn't 15.9Hz.

 

[The Electrician]

Since the numerical differential equation solution is indicating about 15 Hz, and the formula from the Wikipedia page also gives about 15 Hz (15.9 to be exact), it would appear that the differential equation shown in post #2 is correct.

Unless you post your Mathematica work and result I can't help you any further.

 

[Bill Simpson]

If I haven't made a mistake then here is the symbolic solution

In[1]:= r1 = 10^6; c1 = 10*10^-9; r2 = 10^6; c2 = 10*10^-9; r3 = 20*10^3; r4 = 10^4;
DSolve[{v''[t] r4/(r3 + r4) + v'[t]*(r4/(r3 + r4)*(1/(r1*c1) + 1/(r2*c2)) - 1/(r1*c2)) + v[t] (r4/(r3 + r4)*1/(r1*r2*c1*c2)) == 0, v[0] == 1/10, v'[0] == 1/10}, v, t]

Out[1]={{v->Function[{t}, (E^(50*t)*(150*Cos[50*Sqrt[3]*t] - 49*Sqrt[3]*Sin[50*Sqrt[3]*t]))/1500]}}

In[2]:= 50 Sqrt[3]/(2 Pi) // N

Out[2]= 13.7832

 

[d.arbitman]

Since the numerical differential equation solution is indicating about 15 Hz, and the formula from the Wikipedia page also gives about 15 Hz (15.9 to be exact), it would appear that the differential equation shown in post #2 is correct.

Unless you post your Mathematica work and result I can't help you any further.

It should be 15.9 Hz, you're correct. The LTspice simulation gives me 15.9Hz. The Mathcad solution seems to give me ~15Hz. The Mathematica solution seems to give me 50/√3 radians/sec which is equivalent to ~13.8 Hz.

 

[The Electrician]

If I adjust the plot range of the plot of the symbolic solution, I get a plot that looks exactly like the one you have in post#2.

Obviously, the frequency is actually 13.8 Hz. It's not easy to get a good estimate from visual inspection of the plot.

To better see what's going on, let's take the absolute value of the function v[t] (so we don't get any negative values) and do a log plot. That way we have a lot more dynamic range visible. We can see the increase in amplitude over the whole zero to 1 second range of t:

You can see the frequency is approximately 13.8 Hz. But now let's see if we can adjust the gain of the circuit and get the oscillations started by your initial conditions to decay, rather than increasing. I think you may have made an error in your diffeq, but by fooling around with the value of R3 I got what I wanted. For example, if I make R3 equal to 5k ohms, the oscillations decay.

Now, the critical question you're asking is why is the frequency not equal to 15.9 Hz. The reason is found in the behavior of damped systems. See:

http://en.wikipedia.org/wiki/Damping

Notice what they say about the frequency of underdamped systems: "The system oscillates (at reduced frequency compared to the undamped case) with the amplitude gradually decreasing to zero."

The same effect (frequency not equal to the natural frequency, ωo) happens if the system gain is such that the oscillations are increasing in amplitude. Any time the solution consists of a sinusoidal function multiplied by an exponential the frequency will not be ωo.

Here's a plot of the decaying oscillations with R3 set to 5k ohms; now the frequency is 15.4 Hz:

Now with R3 set to 10k ohms the oscillations neither decay nor increase, with a peak amplitude of .1, your initial condition. The solution has no exponential multiplying the sinusoidal part of the solution, and the oscillation frequency is equal to ωo, which is 1/(2 Pi R C) in the case of a Wien bridge circuit):

 

[d.arbitman]

I think you may have made an error in your diffeq, but by fooling around with the value of R3 I got what I wanted. For example, if I make R3 equal to 5k ohms, the oscillations decay.

Now, the critical question you're asking is why is the frequency not equal to 15.9 Hz.

A. I wish I could thank you more than once. You've done a fantastic job.

B. Yes, I was asking why the frequency in the original solution was not 15.9Hz, but I believe that there might be an error with the DiffEq rather than assume damping.

C. Thank you!

 

[The Electrician]

I asked you earlier (post #5) why the amplitude in the (LT spice) simulation was not increasing. I now know that the reason is that LT spice is implicitly using the right differential equation to simulate the circuit. Your component values are giving the right gain (gain of 3) for a Wien bridge oscillator to run without increasing or decreasing amplitude, which is what LT spice shows.

You must have made a mistake in setting up your differential equation involving the circuit gain (R3 and R4; this affects damping), but apparently not in the frequency determining part.

 

[The Electrician]

I found the error in your diffeq--you left out a term. Now with this term included, the oscillations are sustained, no increase or decrease with time, with R3 equal to 20k as expected:

 

[The Electrician]

I notice that what I said in post #12 about solutions with exponential terms having a different frequency than ωo doesn't apply to this Wien bridge oscillator. Changing the value of R3 not only changes the damping, but maintains the frequency constant because it appears in all three of the constant coefficients of the diffeq.

 

[d.arbitman]

I found the error in your diffeq--you left out a term. Now with this term included, the oscillations are sustained, no increase or decrease with time, with R3 equal to 20k as expected:

Can you post how you arrived at that equation? I just want to see the process you went through. I really appreciate all the work you're doing to help me out. :D

EDIT: Never mind. Figured it out!