Difficult mechanics problem - is this even possible to solve?

[Anonymouse]

Problem

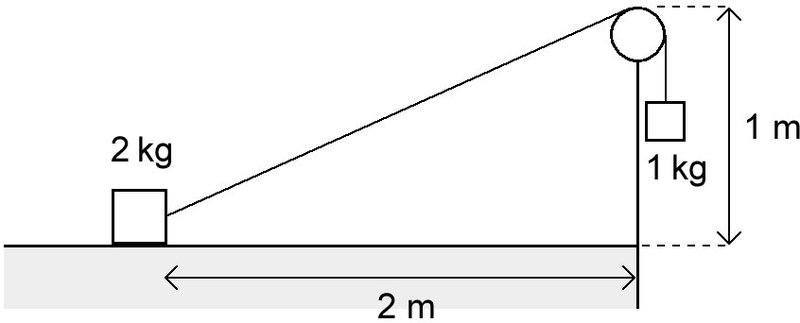
A mass of 2 kg is held at rest on a rough horizontal table with coefficient of friction μ = 0.5. A string is attached to the mass and is hung over a smooth pulley. A 1 kg mass is suspended from the other end of the string. The top of the pulley is at a height of 1 m above the table surface, and the 2 kg mass is initially at a horizontal distance of 2 m away from the pulley as illustrated in the diagram below.

i) Whilst the 2 kg mass is held at rest, what is the tension in the string?

The 2 kg mass is released so that it is free to move across the surface.

ii) What is the tension in the string immediately after the 2 kg mass is released?

iii) How far will the 2 kg mass have moved before it reaches its maximum speed?

Solution

i) This is obvious. If g = 10, then the tension T = mg = 10 N.

This rest is difficult. One needs to find a relation between the acceleration of the two masses, but it is not as straightforward as it seems, because the relative accelerations also depend on the instantaneous velocities and the angle between the relative velocities, right?

Any help appreciated.

 

[denverdoc]

cool problem. Offhand I'd say you need to relate delta x (displacement of horizontal mass) with delta y (vertical mass) and use that to compute the angle of string wrt time, etc.

 

[Mentz114]

Part II is straightforward. If the block is moving then the tension is just the component of the horizontal frictional force along the string. But you need to know the geometry of the block and the attachment in more detail to do the rest ( I think ...).

 

[Anonymouse]

I don't think Part II is straightforward, because you need to relate the acceleration of the 1 kg mass with that of the 2 kg mass. But this relation is not trivial.

If we let the distance between the 2 kg mass and the base of the pulley be x (which starts off at 2 m), and the length of the string between the mass and the pulley be l, then x, l and 1 make a right-angled triangle.

The angle between l and x can be denoted by θ， whence sin θ = 1/l, cos θ = x/l and tan θ = 1/x.

If we take cos θ = x/l, and rearrange to give l cos θ = x, then we can differentiate to get the speeds of the two masses. The speed of the 2 kg mass will be given by dx/dt, and the speed of the 1 kg mass by dl/dt. The problem is that θ is also a variable, which means we have to differentiate that too, so we get something like

dx/dt = dl/dt cos θ - l sin θ

Then to get the relative accelerations, we can differentiate again

d2x/dt2 = d2l/dt2 cos θ - dl/dt sin θ - dl/dt sin θ - l cos θ

I don't know if this is correct so far, but I'll continue.

If I denote the acceleration of the 2 kg mass by A, and that of the 1 kg mass by a, then applying Newton's second law to the 2 kg mass gives

T cos θ - 0.5(20 - T sin θ) = 2A

and to the 1 kg mass gives

10 - T = a

At the beginning, the velocities are zero, so in the equation above, dl/dt = 0, leaving

A = a cos θ - l cos θ

At the beginning, l = 5^-1/2 and cos θ = 2/5^-1/2. Substituting these values and the expressions for a and A into the equation above gives

0.5 T cos θ - 0.25(20 - T sin θ) = (10 - T) cos θ - l cos θ

which can be solved to

T = 8.22 N. Is this the right answer? (Or is there a problem in my method or workings somewhere?)

Part III

The maximum speed will be when the acceleration of the 2 kg mass is zero, so we can replace A by zero in the equation of Newton's 2nd law above. But what about the 1 kg mass? Its acceleration won't be zero, right? So how do we cope with this?

We know T cos θ - 10 + 0.5 T sin θ = 0

but we don't know what T is because the 1 kg mass is still accelerating.

 

[fizzzzzzzzzzzy]

but why would the one kg mass accelerating make a difference? no matter where that mass is or how fast its accelerating, that mass exerts a force of g on the string and therefore on the block. there's probably a faster method than this, but what i would do is use x as the distance between the block and the pulley, figure out the appropriate expressions for the forces, and then make the frictional force equal to the horizontal force.

 

[denverdoc]

but why would the one kg mass accelerating make a difference? no matter where that mass is or how fast its accelerating, that mass exerts a force of g on the string and therefore on the block. there's probably a faster method than this, but what i would do is use x as the distance between the block and the pulley, figure out the appropriate expressions for the forces, and then make the frictional force equal to the horizontal force.

what i had proposed doing was something like:

(m1g-Tsin(theta))cos(theta)*mu=Ff=m1*d"x/dt"
m2g-T=m2*d"y/dt"

and since x^2+1=l dl/dx=-1/2*2x/(x^2+1)=-cos(theta), and dl=dy, using chain rule, and substitution, try to develop explicit equation for only d"x/dt"
ans set equal to zero to find maxima (inflection for velocity), but I keep getting bogged down by rusty calculus skills.

 

[AlephZero]

but why would the one kg mass accelerating make a difference? no matter where that mass is or how fast its accelerating, that mass exerts a force of g on the string and therefore on the block.

No. Think about force = mass * acceleration for the 1kg mass.

The resultant force downwards is mg-T, so mg - T = ma.

If the accleration is 0 (when the mass is at rest) then mg - T = 0 so T = mg.

If the mass was falling freely (accleration = g) then the tension in the string would be 0.

This is one way to attack the last part. When the speed is a maximum, the accleration is 0, and the tension in the string is therefore 10N.

So you have to find the angle of the string, when the 2 kg mass is moving at constant velocity with the string tension and friction acting on it.

For the first part, Anonymouse has got the right idea but you don't need to introduce the angle theta. If the horizontal distance from the table edge is x and the length of the sloping string is l, the acceleration of the two masses are d^x/dt^2 and d^l/dt^2 (since the string is constant length).

By Pythagoras theorem
x^2 + 1 = l^2
Differentiating gives
x dx/dt = l dl/dt
Differentiate again, then use the fact that dx/dt and dl/dt are both zero when t = 0.

I don't have the energy to work out all the details from there on...

 

[MadHawk]

Since, the question involves coefficient of friction and the mass at the surface is double in magnitude, which mathematically yields 8.94N<10N, thus the mass won't move. But if one interchanges the masses then this will have some +ve numerical result.