Rhaegal
Homework Statement
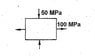
For the state of stress shown in the figure, normal stress acting on the plane of maximum shear stress is?
Homework Equations
Normal stress σn = σcos2θ
3. The Attempt at a Solution
Plane of maximum shear stress is 45o relative to the max stress of 100MPa.
So the total normal stress is 75MPa (compression).
I have assume the direction of normal stresses in both the cases with respect to applied stress.
Have I assumed the direction in both cases correctly?
Thanks in advance!