Direction of a rope with a ball inside an accelerating box

[UnPetitGarcon]

Homework Statement

Calculating the acceleration of a ball attached to a rope attached to the ceiling of a box accelerating along a ramp.

Relevant Equations

F=ma

A steel washer is suspended inside an empty shipping crate from a light string attached to the top of the crate. The crate slides down a long ramp that is inclined at an angle of 37° above the horizontal. The crate has mass 180 kg. You are sitting inside the crate(with a flashlight); your mass is 55 kg. As the crate is sliding down the ramp, you find the washer is at rest with respect to the crate when the string makes an angle of 68° with the top of the crate. What is the coefficient of kinetic friction between the ramp and the crate?

To solve this problem, I drew the free body diagram of the crate first. And from it I came up with an equation: sin(37°) - µcos(37°) = a/g, where a is the acceleration along the ramp and µ the coefficient of friction.

To solve for the a, I then drew the free body diagram of the ball. Here comes the problem: there are two possible directions for the tension.

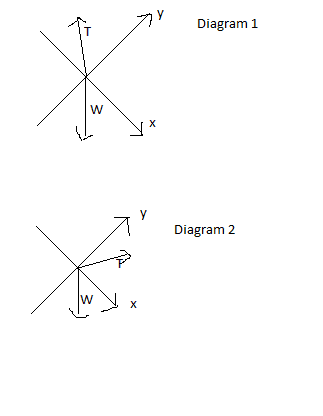
I think both are possible. The second diagram is perfectly reasonable because the tension direction gives a positive value of force along the x direction. When this is combined with the weight in x direction, the net force causes the ball to accelerate down the ramp, which is what exactly happens in the problem. The first diagram is also ok because as long as the x component of the tension is smaller than the x component of the weight, the ball still accelerates down the ramp. So my question is: how to determine which one is correct.

 

[mfb]

In which direction does your crate slide here? Down the x-direction? In that case: In which direction does the washer have to accelerate?

 

[UnPetitGarcon]

In which direction does your crate slide here? Down the x-direction? In that case: In which direction does the washer have to accelerate?

Thanks for reply. Both the crate and the washer slide down the x-direction. But how does it related to the question?

 

[haruspex]

Thanks for reply. Both the crate and the washer slide down the x-direction. But how does it related to the question?

What would be the angle without friction? Does the friction make the washer's acceleration more or less?

 

[UnPetitGarcon]

What would be the angle without friction? Does the friction make the washer's acceleration more or less?

Got it! So Diagram 1 is the correct one because it makes the washer's acceleration less compared to the situation without friction. Thank you very much.

 

[haruspex]

Got it! So Diagram 1 is the correct one because it makes the washer's acceleration less compared to the situation without friction. Thank you very much.

Right.