Biker
- 416
- 52
Homework Statement
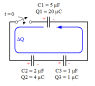
Assume you have C1, C2, C3 capacitors and each one of them have a specific charge. Now imagine you connect them to one circuit (Just as in the picture below). Determine the charge on each capacitor after the movement of charges stop
Homework Equations
Kirchhoff's law
The Attempt at a Solution
So when I started solving these problems, I came out with a good solution for these problems.
Now the basic solution for a charged capacitor to charge another capacitor is to consider those in parallel, But here we just cant.
So my solution has always showed the right answers, I wonder if it does apply here too.
Basically, you show that one of the capacitors (c1) has a voltage bigger than the sum of others thus a current will pass. Now I can say that Q charges will move in the whole period and with the indicated polarities above I can say that C1's charges decreases by Q and C2's charge increase by Q and C3's charges increase by Q
Now by using conservation of energy or Kirchhoff's 2nd law (voltage law) you can actually determine Q
and you can then get the charge of each capacitor after charging.
It gave sensible answer, that gave me a round trip of zero