Discrepancies between numerical and analytical solutions

[Ziezi]

The analytical solutions are:
\begin{equation}
\psi(x) =
\begin{cases}
Ce^{\alpha x}, \text{if } x < -\frac{L}{2}\\
Asin(kx) + Bcos(kx), \text{if } -\frac{L}{2} \leq x \leq \frac{L}{2}\\
Fe^{-\alpha x} , \text{if } x > \frac{L}{2}
\end{cases}
\end{equation}
Next, $\psi(x)$ must be continuous and differentiable, which means that the value of the functions and their derivatives must match at the boundaries, $-\frac{L}{2}$ and $\frac{L}{2}$. Depending on whether the solution is symmetric, $\psi(-x) = \psi(x)$, or anti-symmetric, $\psi(-x) = -\psi(x)$, $A = 0$, $C = F$ or $B = 0$. $C = -F$, respectively. For the symmetric case:
\begin{equation}
\begin{array}{|l@{}}
Fe^{-\alpha L/2} = Bcos(k L/2)\\
-\alpha F e^{-\alpha L/2} = -\alpha Bcos(k L/2)
\end{array}
\end{equation}
taking the ratio of the above two give us $\alpha = k tan(k L/2)$. Similarly, from the anti-symmetric case we get $\alpha = -k cot(k L/2)$.Both $\alpha$ and $k$ depend on the energy, $E$, making the above equations transcendental. To solve them we make the following substitutions:
\begin{equation}
\begin{array}{|l@{}}
\eta = \frac{L}{2}\frac{\sqrt{2mV_0}}{\hbar}\\
\xi = \frac{L}{2}\frac{\sqrt{2mE}}{\hbar} = k \frac{L}{2} \quad (1)
\end{array}
\end{equation}
With a small rearrangement our equations for the symmetric and anti-symmetric become:
\begin{equation}
\begin{array}{|l@{}}
\alpha = k tan(k L/2) \iff \sqrt{\frac{\eta^2}{\xi^2} - 1} = tan(\xi)\\
\alpha = -k cot(k L/2) \iff \sqrt{\frac{\eta^2}{\xi^2} - 1} = -cot(\xi)
\end{array}
\end{equation}
To calculate the above I use the following Octave code:

    x = -6 : 0.1 : 46;                                  % coordinates  interval.
    w = 1;                                              % well width.
    U_0 = 40;                                           % well depth.
    hbar = 1;                                           % Planck's constant.
    m = 1;                                              % particle mass.
 
    eta = ( w*sqrt(2*m*U_0) ) / (2*hbar);   xi = @(E) ( w*sqrt(2*m * E) ) / (2*hbar);
    lhs = @(E) sqrt( ( (eta*eta) ./ (xi(E).^2) )  - 1);
    rhs_s = @(E) tan( xi(E) );                          % symmetric case.
    rhs_a = @(E) -cot( xi(E) );                         % anti-symmetric case.

    % Solve the transcendental equation using root-finding algorithm.
    func_1 = @(E) lhs(E) - rhs_s(E);  func_2 = @(E) lhs(E) - rhs_a(E);

    x_0_s = 2;                              x_0_a =  10;
    root_xi_x_s = fzero(func_1, x_0_s);     root_xi_x_a = fzero(func_2, x_0_a);
    root_xi_y_s = real(rhs_s(root_xi_x_s)); root_xi_y_a = real(rhs_a(root_xi_x_a));
 
    E_0 = (2*root_xi_x_s^2) / (m * w^2); E_1 =  (2*root_xi_x_a^2) / (m * w^2)   

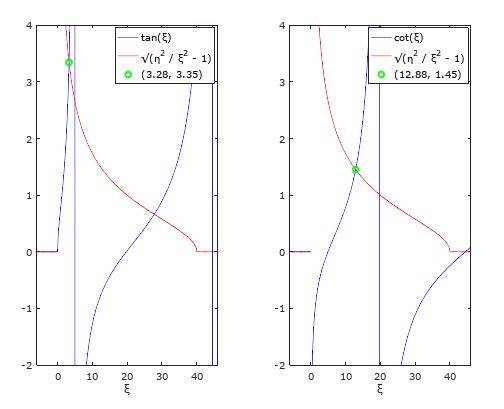
    subplot(1, 2, 1);
    plot(x, real(rhs_s(x)), 'b', x, real(lhs(x)), 'r', root_xi_x_s, root_xi_y_s, 'go')
    axis([-6 46 -2 4])'; xlabel('\xi');
    label3 = ['(', sprintf("%.2f", root_xi_x_s), ', ', sprintf("%.2f", root_xi_y_s), ')'];
    legend('tan(\xi)', '\surd(\eta^2 / \xi^2 - 1)', label3);

    subplot(1, 2, 2);
    plot(x, real(rhs_a(x)), 'b', x, real(lhs(x)), 'r', root_xi_x_a, root_xi_y_a, 'go')
    axis([-6 46 -2 4]); xlabel('\xi');
    label4 = ['(', sprintf("%.2f", root_xi_x_a), ', ', sprintf("%.2f", root_xi_y_a), ')'];
    legend('cot(\xi)', '\surd(\eta^2 / \xi^2 - 1)', label4);

From $$(12)$$ and the two values for $$\xi$$, the results for the energies are:
> 331.98<br>
> 21.50<br>

Now, for the numerical solution I use the following:

    % Parameters for solving problem in the interval -L < x < L.
    L = 5;                                               % Interval Length.                                                                                                                       
    N = 1000;                                            % No of points.
    x = linspace(-L, L, N)';                             % Coordinate vector
    dx = x(2) - x(1);                                    % Coordinate step

    % Finite square well of width 2w and depth given by U_0.
    U_0 = 40;                           w = L / 10;                                 
    U = -U_0*(heaviside(x + w) - heaviside(x - w));

    % Discretized (three-point finite-difference) representation of the Laplacian.
    e = ones(N, 1);                                             
    Lap = spdiags([e  -2*e e], [-1 0 1], N, N)

    % Total Hamiltonian
    hbar = 1;                                                         
    m = 1;                                                             
    H = -1/2*(hbar^2 / m)*Lap + spdiags(U, 0, N, N);  % T = H + U.

    % Find (first 3) (smalest algebraic) eigenvalues.
    nmodes = 3;             options.disp = 0;
    [V, E] = eigs(H, nmodes, 'sa' , options);   
    [E, ind] = sort(diag(E));                   
    E

The results for the energies are:
>36.72<br>
>27.14<br>
>12.27

I'm expecting some error but in this case, the energies differ in an order of magnitude.

Clearly, I am doing something wrong but I don't know whether the error is in the analytical or numerical solution. What am I doing wrong here? Any hint will be appreciated.

---

 

[kuruman]

I am not a MATLAB expert, but I know enough to suggest putting the two sets of solutions back into your equations (4) and see which one (if any) satisfies them.

 

[Ziezi]

I am not a MATLAB expert, but I know enough to suggest putting the two sets of solutions back into your equations (4) and see which one (if any) satisfies them.

That is not a bad idea, however, equation (12) is useful assuming that the values of $\xi$ are valid. The second value of $\xi$ produces an energy, $E = 331.98$, making it a bit ambiguous given that the potential is only $U_0 = 40$.

Most probably there are mistakes in both, analytical and numerical, methods.

 

[kuruman]

Wait a minute. Look at your equations (3). What are your definitions of $k$ and $\alpha$? If this is a particle in a finite square well problem, then if you redefine dimensionless constants $\eta$ and $\xi$, it must be true that $\eta^2+\xi^2 = const.$

 

[Ziezi]

Wait a minute. Look at your equations (3). What are your definitions of $k$ and $\alpha$? If this is a particle in a finite square well problem, then if you redefine dimensionless constants $\eta$ and $\xi$, it must be true that $\eta^2+\xi^2 = const.$

You are right, I've omitted a crucial part:

Inside the box, the wavefunction is:

\begin{equation}
\frac{\hbar^2}{2m} \frac{d^2 \psi(x)}{dx^2} = E \psi(x) \iff
\frac{d^2 \psi(x)}{dx^2} = k^2 \psi(x)
\end{equation}
where $k = \frac{\sqrt{2mE}}{\hbar}$. Outside the box:
\begin{equation}
-\frac{\hbar^2}{m} \frac{\partial^2 \psi(x)}{\partial x^2} = (E - V_0) \psi(x) \iff \frac{\partial^2 \psi(x)}{\partial x^2} = \alpha^2 \psi(x)
\end{equation}
where $\alpha = \frac{\sqrt{2m(V_0 - E)}}{\hbar}$.P.S.: I can't edit the OP more. So, I'm placing what should be at the beginning as a response