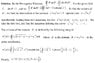- #1
s3a
- 818
- 8
Homework Statement
Find the outward flux of the radial vector field F(x,y,z) = x i^ + y j^ + z k^ through the boundary of domain in R^3 given by two inequalities x^2 + y^2 + z^2 ≤ 2 and z ≥ x^2 + y^2.
Homework Equations
Divergence theorem: ∫∫_S F ⋅ n^ = ∫∫∫_D div F dV
The Attempt at a Solution
Is the final answer correct in TheSolution.jpg (because I get 2*pi/3 * (2^(3/2) - 1) - pi/2)?
If someone could check if I'm right or wrong, I would REALLY appreciate it!