Do I have enough thread strength for my bolt system to withstand a force?

[Dafe]

Hey, I'm trying to learn a bit about the strength of threads in bolts and have a couple of questions.

Let's say I have a system that looks something like this:

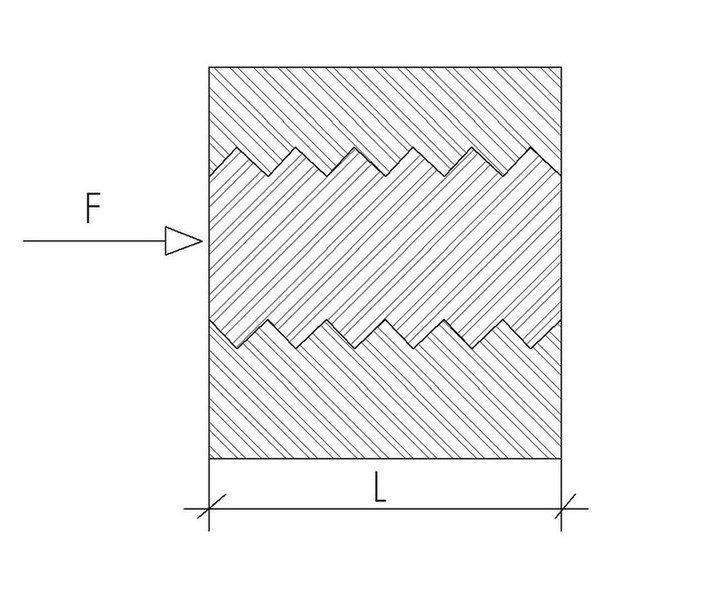
I want to find out if there are enough threads to withstand the force F.

The nut and bolt material are not the same.

I have done some research and found out that ANSI has a couple of equations for this type of analysis.

First we have the Shear Area of External Threads :
A_s,e = pi*n*L_e*K_nmax*[1/2n + 1/sqrt3*(E_s,min-K_nmax)]
where
n=threads/inch
L_e=Length of engagement
K_nmax=maximum inner diameter of nut
E_s,min=minimum pitch diameter of bolt

I really don't understand this equation. This is supposed to be the area where shear will occur right? How is it that they use the length of engagement to get that area?
Can I divide the force F with this area and compare the results with the shear strength of the material?

I know, a lot of questions, hope someone can give me some hints.

Thank you

 

[Astronuc]

The term (K_nmax*[1/2n + 1/sqrt3*(E_s,min-K_nmax)]) would be the effective diameter per unit length of engagement.

So the engagement area would be effective circumference * L_e, where effective circumference = pi * effective diameter. The location of maximum shear is not necessarily at the base of the thread, and is not necessarily parallel with the axis of the bore.

 

[Dafe]

I think that if the nut material is stronger than the material from which the bolt is made, the threads will strip at the roots of the bolt teeth. Doesn't that mean that the location of maximum shear will be at the base of the thread?
Thanks a lot for breaking down the equation for me!

 

[FredGarvin]

The nut and bolt material are not the same.

That is a good thing. In a proper design, the nut should be stronger than the bolt. A general rule of thumb is that you want the nut's proof strength to be greater than than or equal to the bolt's ultimate strength. This is worked into nuts and bolts of the same standard. The nuts will have a greater strength so as to develop the maximum load of the bolt. You want this, mainly, because a stripped bolt is MUCH easier to detect than a stripped nut.

I have done some research and found out that ANSI has a couple of equations for this type of analysis.

First we have the Shear Area of External Threads :
A_s,e = pi*n*L_e*K_nmax*[1/2n + 1/sqrt3*(E_s,min-K_nmax)]
where
n=threads/inch
L_e=Length of engagement
K_nmax=maximum inner diameter of nut
E_s,min=minimum pitch diameter of bolt

I really don't understand this equation. This is supposed to be the area where shear will occur right? How is it that they use the length of engagement to get that area?

That's the standard for calculating the stripping of a thread form. The reason the length of engagement is involved is because the longer the thread engagement, the more stripping area is created. Imagine you are calculating the area of compound circles. Each thread is a circle and each thread's circle adds to the overall stripping area. This is why, in tables, thread stripping areas are tabulated for a length of engagement equal to the nominal diameter of the thread. If you think about it, this makes perfect sense. If the length of engagement were not involved, why would we need different lengths of bolts?

Can I divide the force F with this area and compare the results with the shear strength of the material?

It depends. If you get the area from a table that lists them, as I just mentioned, that area is based on a length of engagement equal to one diameter of the thread.

 

[Dafe]

The nut has a tensile yield strength of 515Mpa while the bolt has a Tensile ultimate strength of 345Mpa.

I used the equation with a length of engagement a bit larger than the nominal diameter of the thread. I got A_ts=970mm^2.

Then the force required to strip (shear) the thread of a bolt or nut:

F=S_u*A_ts where S_u=ultimate shear strength of the nut or bolt material

The bolt is made of Titanium Grade 2 and I don't know its ultimate shear strength. What I do is say that the ultimate shear strength is 0.6*yield strength, just to be on the safe side. Is this alright?

I get a force much larger than the force that is going to be applied to the bolt. Would this be proof enough that the bolt and nut will hold?

Thank you!

 

[FredGarvin]

The 60% for shear is good for ductile materials. I would have to go back into my references to see if that holds for Ti. Come to think of it, you don't need the shear strength. Use the ultimate tensile of the material for your calculations. That is what is done in the literature.

You're on the right track. The thing about fasteners is that they can be infinitely complicated if you so choose. They seem very simple but they really are not. The calculation you have done is a good start. To do a full fastener analysis, you need to look at the possible shear loads on the bolts, the preload applied and the possibility of an induced bending moment in the fasteners.

If you want to be absolutely certain about your fasteners, make sure you have a good factor of safety built in, like FS=3 on yield. That will be very conservative.

 

[Dafe]

Would you mind explaining how come I don't need the shear strength?
I think the preload in my particular case is so small that I can look past it.

Since I have used 0.6*yield to calculate the force needed to strip the threads, and the fact that the force is many times larger than the force I will apply the fastener, I think I may say that the fastener will hold. Do you agree?

Thank you for your time!

 

[FredGarvin]

The thing usually looked at is the tensile failure of the shank itself. If you really want to try to calculate the thread stripping (which should happen AFTER the shank fails in a proper design) you would indeed look at the shear strength. I just always assume one is talking about the tensile failure. Sorry for the confusion.

I would be careful with neglecting preload. I have no idea what your joint or loading looks like so it's your call. Usually preload is specified around 70% of yield in a standard situation.

 

[Dafe]

I have found a equation for the tensile stress area of a fastener:

A_t = pi/4[(d_b - (0.9743/n)]^2

where
d_b = diameter of bolt
n=1/p=threads/in

Is it a good idea to use this to find the tensile stress in the bolt caused by the force F (in the drawing)?

I do find all this quite confusing actually.
For example, there is one equation for tensile strength which uses the average of the root and pitch diameter. Then there is the stress area I wrote above.
And to top it all the length of engagement for when the materials are of unequal strength is a ratio of the tensile area, the tensile strength of external threads, shear area of internal threads and the shear strength of internal threads! They don't even mention the force put on the bolt!

Sorry for my rant there :) Thanks again

 

[jaap de vries]

You need to make sure that the thread engagement is large enough. If its not or less than the nominal diameter of the bolt then you need to take into account that the load distribution over your individual threads is probably not going to be equal. Let me know if this is the case because I have a method from the ASME boiler and pressure vessel code book that deals with that.

 

[FredGarvin]

I have found a equation for the tensile stress area of a fastener:

A_t = pi/4[(d_b - (0.9743/n)]^2

where
d_b = diameter of bolt
n=1/p=threads/in

Is it a good idea to use this to find the tensile stress in the bolt caused by the force F (in the drawing)?

I do find all this quite confusing actually.
For example, there is one equation for tensile strength which uses the average of the root and pitch diameter. Then there is the stress area I wrote above.
And to top it all the length of engagement for when the materials are of unequal strength is a ratio of the tensile area, the tensile strength of external threads, shear area of internal threads and the shear strength of internal threads! They don't even mention the force put on the bolt!

Sorry for my rant there :) Thanks again

That tensile area is the tensile area of the shank. If you run the numbers between the two methods, the area should come out to be equal. I have a spreadsheet that does this for a few methods and the fasteners I have looked at this is the case. There may be some that are slightly different, but they are going to be very close.

The force on the bolt isn't really needed in these calculations. It all comes down to the areas involved until you get to the failure theory of things in which case you do need the force.

Jaap,
Even if you do have the required length of engagement, the load is never evenly distributed over all of the threads. The rule of thumb is that the first 4 threads take a good portion of the loading.

 

[FredGarvin]

I would highly receommend that you get a copy of Bickford's Introduction to the Design and Behavior of Bolted Joints. It does a very good job of explaining and showing just how very difficult fastener design and analysis can be.

 

[nucleus]

A couple other sources of online information are the NASA design manual available at the bottom of the page here:
http://gltrs.grc.nasa.gov/cgi-bin/GLTRS/browse.pl?1990/RP-1228.html
and the Bolt Science site:
http://www.boltscience.com/

 

[FredGarvin]

That fastener design manual is good, but a bit on the confusing side. Nasa also has a couple of others linked to space systems listen in its references section. They are definitely worth looking through.

 

[araanandv2]

Thank you all. Good Explanation

My query:
How do you calculate the Le(thread length engagemnet)

the formual given is (linK below)
http://www.engineersedge.com/thread_strength/thread_minimum_length_engagement_fed-std-h28.htm

But our senior engineers use
shear strength=load/((pi*pitch dia*thread length)/2),

We know the shear strength (.60 of yield strength of the material)
load and pitch dia. we then calculate the thread length.

Could you please explain which one we need to follow?

Thanks,

Ana

 

[Dafe]

Great posts!

I have now calculated the shear area of external threads and the tensile area.
Then I divided my force with the areas and compared the results with 0.6*yield and yield, respectively.
I've talked to some people and they said that the pretension is not going to be a huge factor.

I now understand that fastener design is a tricky one, and I'll sure look into the references you've provided.

For now, I think these simple calculations I've done will do the trick.

Feel free to add more references, or good tips :) thank you very much