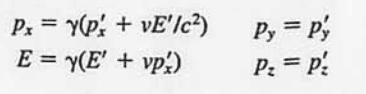PeroK said:
Yes, in fact the energy-momentum of a photon is an eigenvector of the Lorentz Transformation; and, the Doppler red and blue-shift factors are the eigenvalues!
That's only true if the boost (it's not a general Lorentz transform being discussed here but a boost) is in the direction of the photon's momentum. Indeed, a boost has two space-like and two light-like eigenvectors. For simplicity take a boost in ##x## direction as mentioned in #1. It's representing matrix is given by
$$\Lambda=\begin{pmatrix} \cosh \eta & -\sinh \eta &0 &0 \\ -\sinh \eta & \cosh \eta &0 &0 \\ 0 & 0 & 1 & 0 \\ 0&0&0&1 \end{pmatrix}.$$
Obviously the two space-like vectors ##(0,0,1,0)## and ##0,0,1,0## are eigenvectors with eigenvalue 1 of this matrix.
The other two must be in the ##x^0x^1## plane, because the eigenvalues must be Minkowski-orthogonal to the already found eigenvectors. It's easy to see that these are the two light-like vectors
$$a^{\pm}=\begin{pmatrix}1 \\ \pm 1 \\0 \\0 \end{pmatrix}.$$
That corresponds to photons, one running in the positive the other in the negative ##x^1## direction. The eigenvalues found by
$$\Lambda a^+=(\cosh \eta - \sinh \eta) =\exp (-\eta) a^+, \quad \Lambda a^-=(\cosh \eta + \sinh \eta) a^-=\exp \eta a^-.$$
These are indeed the Doppler factors for the longitudinal Doppler effect, because we have
$$\beta=\frac{v}{c} = \tanh \eta$$
and thus
$$\exp(\mp \eta)=\frac{\cosh \eta \mp \sinh \eta}{\sqrt{\cosh^2 \eta - \sinh^2 \eta}} = \frac{1 \mp \beta}{\sqrt{1-\beta^2}} = \sqrt{\frac{(1 \mp \beta)^2}{(1+\beta)(1-\beta)}} = \sqrt{\frac{1 \mp \beta}{1\pm \beta}}.$$
So if the boost is in direction of the photon (upper sign for ##\beta>0##) we have a red shift (energy in the new frame larger than in the original), otherwise a blue shift.
In the general case, i.e., when the boost is not in direction of the photon's motion, you have a Doppler shift and in addition an aberration of the photon's direction!