- #1
ABW
- 13
- 0
In GR gravity is associated with the curvature of space caused by the presence of massive bodies.
Along with GR, there is an approach in which the gravitational field
- is a real physical field, whose properties can be described by equations,
similar to the Maxwell equations for electromagnetic field.
Differential equations for the gravitational field
Part 1. Maxwell's equations for the electromagnetic field can be supplemented by the differential equations for the gravitational field :
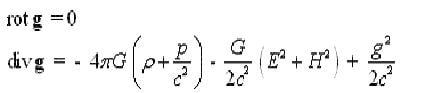
The second equation describes the sources of the gravitational field: It is a common substance with density "Rho" , the electromagnetic field with intensity E and H , and the gravitational field strength g , ( g is the dimension of acceleration ), p is the pressure . The fact, that the gravitational field as any kind of matter, can be a source of gravity , while nobody was paying attention . G is Newton's constant . c - is the speed of light .
From equations we find formula for the energy density of the gravitational field :
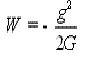
Unexpected in this expression is that the gravitational constant G is in the denominator .
Compare this expression with the energy density of electric and magnetic fields in vacuum:
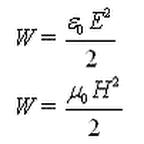
So for the gravitational field at the surface of the Earth g = 9.81 m/sec2 , we find :
W ~ - 10^11 Jowl/m3 . The sign “-” in the formula for the energy density of the gravitational field indicates that the energy density, and the corresponding energy of gravitational interaction is negative.
It is easy to give a formula for refined Newton's law, taking into account, that the gravitational field is also a source of gravitation :
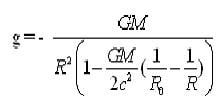
M is the mass of the body , Ro is the radius of the body.
The gravitational field at large distances is higher compared to the classical value.
This formula can in our opinion to explain why the space station “pioneer-10 ”, NASA , currently outside the Solar system slows down faster than it should of calculations . Here is what says about this journal Relcom.ru : “Movement "Pioneer 10" in the space of interested scientists since it was discovered that the observed deceleration cannot be explained alone by the gravitational pull of the Solar system. It can serve as evidence for the existence of an as yet unknown to science forces, or associated with any properties of the spacecraft .”
Along with GR, there is an approach in which the gravitational field
- is a real physical field, whose properties can be described by equations,
similar to the Maxwell equations for electromagnetic field.
Differential equations for the gravitational field
Part 1. Maxwell's equations for the electromagnetic field can be supplemented by the differential equations for the gravitational field :
The second equation describes the sources of the gravitational field: It is a common substance with density "Rho" , the electromagnetic field with intensity E and H , and the gravitational field strength g , ( g is the dimension of acceleration ), p is the pressure . The fact, that the gravitational field as any kind of matter, can be a source of gravity , while nobody was paying attention . G is Newton's constant . c - is the speed of light .
From equations we find formula for the energy density of the gravitational field :
Unexpected in this expression is that the gravitational constant G is in the denominator .
Compare this expression with the energy density of electric and magnetic fields in vacuum:
So for the gravitational field at the surface of the Earth g = 9.81 m/sec2 , we find :
W ~ - 10^11 Jowl/m3 . The sign “-” in the formula for the energy density of the gravitational field indicates that the energy density, and the corresponding energy of gravitational interaction is negative.
It is easy to give a formula for refined Newton's law, taking into account, that the gravitational field is also a source of gravitation :
M is the mass of the body , Ro is the radius of the body.
The gravitational field at large distances is higher compared to the classical value.
This formula can in our opinion to explain why the space station “pioneer-10 ”, NASA , currently outside the Solar system slows down faster than it should of calculations . Here is what says about this journal Relcom.ru : “Movement "Pioneer 10" in the space of interested scientists since it was discovered that the observed deceleration cannot be explained alone by the gravitational pull of the Solar system. It can serve as evidence for the existence of an as yet unknown to science forces, or associated with any properties of the spacecraft .”