Does the "space twin" benefit from length contraction?

[Peter Martin]

Does the “space twin” benefit from length contraction as well as time dilation?

In Einstein’s thought experiment, let one of twins travel to a galaxy known to be 10 light years from Earth at a speed of sixty percent of light speed (0.6c). Were it not for time dilation the one-way trip would take him 10 light years divided by 0.6 light years per year, or 16.7 years.

But because, for him, time passes at only 80% of time on Earth, he experiences the passage of only 13.3 years. Thus on return, he has aged 26.6 years while his “Earth twin” has aged 33.3 years.

But for the space twin, the galaxy is only 8 light years distant due to length contraction. So his round-trip travel time is only 21.3 years.

Does he benefit from both time dilation and length contraction?

 

[Dale]

Does he benefit from both time dilation and length contraction?

Certainly both length contraction and time dilation occur. However, whether it is a “benefit” or not depends on the goal.

 

[PeroK]

Does the “space twin” benefit from length contraction as well as time dilation?

In Einstein’s thought experiment, let one of twins travel to a galaxy known to be 10 light years from Earth at a speed of sixty percent of light speed (0.6c). Were it not for time dilation the one-way trip would take him 10 light years divided by 0.6 light years per year, or 16.7 years.

But because, for him, time passes at only 80% of time on Earth, he experiences the passage of only 13.3 years. Thus on return, he has aged 26.6 years while his “Earth twin” has aged 33.3 years.

But for the space twin, the galaxy is only 8 light years distant due to length contraction. So his round-trip travel time is only 21.3 years.

Does he benefit from both time dilation and length contraction?

He isn't shorter when he gets back to Earth, if that is what you are asking.

 

[Ibix]

galaxy known to be 10 light years from Earth

That's a very nearby galaxy - the things are typically 10,000 light years across. Perhaps you mean a star system?

But for the space twin, the galaxy is only 8 light years distant

This is his explanation for why his clocks show less time - the star was doing 0.6c, but it didn't travel as far as the Earth frame says he did.

 

[Wes Tausend]

Does the “space twin” benefit from length contraction as well as time dilation?

In Einstein’s thought experiment, let one of twins travel to a galaxy known to be 10 light years from Earth at a speed of sixty percent of light speed (0.6c). Were it not for time dilation the one-way trip would take him 10 light years divided by 0.6 light years per year, or 16.7 years.

But because, for him, time passes at only 80% of time on Earth, he experiences the passage of only 13.3 years. Thus on return, he has aged 26.6 years while his “Earth twin” has aged 33.3 years.

But for the space twin, the galaxy is only 8 light years distant due to length contraction. So his round-trip travel time is only 21.3 years.

Does he benefit from both time dilation and length contraction?

Good question. Have we ever even resolved the twin paradox here on PF without this complication?

Wes
...

 

[Mister T]

But because, for him, time passes at only 80% of time on Earth, he experiences the passage of only 13.3 years. Thus on return, he has aged 26.6 years while his “Earth twin” has aged 33.3 years.

That's an explanation provided by the staying twin.

But for the space twin, the galaxy is only 8 light years distant due to length contraction. So his round-trip travel time is only 21.3 years.

Yup, that's an explanation provided by the traveling twin.

Does he benefit from both time dilation and length contraction?

What happens to him occurs because he took a shorter path through spacetime. That's one way to explain it. As are the above two explanations. The advantage to the spacetime path explanation is that it's an explanation that can be provided by both twins. It resolves the paradox whereas the other two explanations require additional considerations to explain why it's the traveling twin, and not the staying twin, who ages less.

 

[laymanB]

But for the space twin, the galaxy is only 8 light years distant due to length contraction. So his round-trip travel time is only 21.3 years.

The distance due to length contraction is indeed 8 light years for the space twin, but he is still traveling at 0.6c relative velocity (both the Earth twin and space twin will agree on this). So you have to use the same logic to calculate the entire journey time as measured by the space twin.

16 light years / 0.6c = 26.6 years.

The same results as figured from the time dilation by the Earth twin. The Earth twin's explanation is that the space twin's clock was slow, the space twin's explanation was that it wasn't as far as they originally thought. So to answer your question of whether the space twin can use time dilation and length contraction, the answer is no; they are not additive. That would imply that the space twin's clock that is at rest in his spaceship was actually running slower by 80%, which it is not according to him.

 

[pervect]

Does the “space twin” benefit from length contraction as well as time dilation?

In Einstein’s thought experiment, let one of twins travel to a galaxy known to be 10 light years from Earth at a speed of sixty percent of light speed (0.6c). Were it not for time dilation the one-way trip would take him 10 light years divided by 0.6 light years per year, or 16.7 years.

But because, for him, time passes at only 80% of time on Earth, he experiences the passage of only 13.3 years. Thus on return, he has aged 26.6 years while his “Earth twin” has aged 33.3 years.

But for the space twin, the galaxy is only 8 light years distant due to length contraction. So his round-trip travel time is only 21.3 years.

Does he benefit from both time dilation and length contraction?

Let's consider a hypothetical scenario where the traveling twin's clock reads half the time that the stationary twin's clock reads.

THen the traveling twin calculates the time for the trip as the length contracted distance divided by his velocity, and the length contraction is 2, and the velocity is the same in both frames of reference, so he arrives in half the time. The non-travelling twin doesn't see any length contraction of the trip, but he does compute the time dilation for the traveling twin as being 2:1, so that's his explanation for the shorter time reading on the traveling twin's clock.

THe explanation for how the traveling twin explains the *longer* time reading of the non-travelling twin's clock involves an effect which you haven't mentioned, called the relativity of simultaneity. It's not clear if you're asking about that effect, so I won't say anything more without prompting.

 

[Wes Tausend]

...

I think ship acceleration plays a major role too. See the second paragraph in the wikipedia Twin Paradox. There appears to be more than one school of thought amongst the experts, which is why I earlier asked if PF had any 'official paradox consensus' that we must adhere to.

I wonder, wouldn't the traveling twin's trip away from the stationary twin cause time to slow down, whereas the traveling twin's trip coming back, cause time to speed up? Considering observed red shift effects, this seems a distinct possibility.

My reasoning follows:
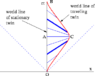
I think the stationary twin can frankly observe the ship clock rate changes by watching a light mounted upon the leaving spaceship that was originally matched in frequency to the other twin's companion light on earth. Comparatively, from earth, the ship's light should slow in frequency (red shift) along with the exact earth-perceived clock rate aboard ship. When the spaceship briefly stops to return, the ship light frequency, now temporarily relative (equal) to Earth's inertial frame, should briefly run at the same time as Earth (no red shift); i.e. the light frequency on Earth and all included clocks should temporarily agree as to rate.

When the spaceship reverses to return and begins to move, the ship light should now display a blue shift as seen from earth, indicative of the ships new faster (than earth) clock rate. From this, it seems logical to me, while going away the ship's clock should run slower than Earth's clock... and returning, run faster... just enough to cancel any brotherly time difference after the traveling twin has returned. In this discussion, I believe we are talking about pure radial motion straight out and straight back, not transverse (tangential) motion (two ships passing nearby, along side one another for instance) where any relative motion may cause slightly different time effects.

Besides the specific inertial travel frames to be considered, are also accelerated frames to allow the ship to take off and eventually reverse direction back towards Earth with distant accompanying deceleration and re-acceleration, then finally deceleration again to land at home. In carefully considering these accelerations, it seems the permanent net time difference should then still be null (just as any permanent length contraction occurs then becomes null). With permission, I think I might be able to heuristically demonstrate this more elaborately (including contractions) in a rocket thought experiment using two ship clocks, triplets, SR and different effects of acceleration in rotation and non-rotation of the ship and occupants. The ship rotation (front to back) may momentarily change how the clocks work if the ship does rotate.

Keep in mind that in SR, a forward ship clock does not run at the same time as the rearward ship clock during acceleration-like phases, just as occurs in gravitational time dilation (because of equivalence). The acceleration itself does not affect the clock, but the rate of a clock does depend on its equivalent instantaneous velocity which is under continuous change during any acceleration.

I feared to suggest this here. It is apparent I do not entirely agree with everybody else on the Twin Paradox. As I walk on eggs, I hope they do not break. I sure hope this makes sense (follows logical steps) to others that may read this. I hope it regarded either as an insight, or at least, if I'm dead wrong in my logic, a harmless misconception.

Wes
...

 

[Peter Martin]

I thank everyone for their input to my query on the twins paradox. As for length contraction shortening the distance to the target star (not galaxy, thank you ibix) while in inertial motion the space twin can detect neither time dilation nor length contraction aboard his spacecraft . So for him, the star appears to be the full 10 light years away, not 80% of that.

Now I’m wondering if he sets off a brilliant flash upon arriving at the star, when would his Earth twin see it, taking the propagation of the flash into consideration?

 

[Ibix]

while in inertial motion the space twin can detect neither time dilation nor length contraction aboard his spacecraft . So for him, the star appears to be the full 10 light years away, not 80% of that.

For the traveller, the star is in inertial motion. One could build a rod from star to star with rest length 10ly. To the traveller, it would be in motion at 0.6c, so length contracted. As would the distance between stars.

 

[Mister T]

So for him, the star appears to be the full 10 light years away, not 80% of that.

No, he would observe that the distance to the star is Lorentz contracted, that is, shorter than the proper distance.

Now I’m wondering if he sets off a brilliant flash upon arriving at the star, when would his Earth twin see it, taking the propagation of the flash into consideration?

10 years later.

 

[Ibix]

Now I’m wondering if he sets off a brilliant flash upon arriving at the star, when would his Earth twin see it, taking the propagation of the flash into consideration?

When according to who? According to the stay-at-home, it took 16.7 years for the traveller to get there. It takes 10 years for the signal to cross 10ly. Easy.

According to the traveling twin, Earth is approaching at 0.6c. It takes T years for the pulse to arrive at Earth. In that time, Earth travels 0.6T light years and the signal travels T light years. The total when they meet must be eight light years. So 0.6T+T=8, so five years after the signal is sent.

 

[Nugatory]

Mentors' note:

A long digression about how to properly understand the role of acceleration in the twin paradox has been removed from this thread. Any further discussion of that question should happen in a new thread; and if someone wants to start that thread they should first work through the various acceleration-free versions of the twin paradox that have been discussed in other threads here over the years.

The thread cleanup has taken removed a number of thoughtful posts that doubtless took a fair amount of effort to write. Anyone who wants a copy of their post for reference or possible future use can ask any of the mentors for a copy.

 

[PeterDonis]

See the second paragraph in the wikipedia Twin Paradox. There appears to be more than one school of thought amongst the experts, which is why I earlier asked if PF had any 'official paradox consensus' that we must adhere to.

There might be more than one school of thought among the experts about pedagogy--how to present the twin paradox to lay people or beginning students of SR--but there is only one "school of thought" about what SR predicts.

Any further discussion of this (in a new thread, as @Nugatory has pointed out) should definitely be informed by the Usenet Physics FAQ article on the twin paradox:

http://math.ucr.edu/home/baez/physics/Relativity/SR/TwinParadox/twin_paradox.html

This does an excellent job of (a) describing various possible ways of analyzing the paradox, (b) showing how they all give the same predictions, (c) distinguishing between how each twin describes the events using coordinates (which is what is usually discussed) and what each twin directly observes with their eyes or telescopes or instruments (the "doppler shift analysis" section of the article), and (d) providing the most general analysis that subsumes all the others (what the article calls the "spacetime diagram analysis") and which is also the analysis that generalizes to cases where gravity is not negligible, i.e., to general curved spacetimes in GR as well as flat spacetime in SR.

 

[Wes Tausend]

A nights sleep helped me resolve my issue in a clear manner, so I have nothing further to add except some thanks and an apology. Thanks to the individuals that helped me see and thanks to the moderators for not permanently locking a worthy thread on my account. They are called Mentors for good reason and I appreciate the guiding hand. I apologize to all for the fumbling post.

Wes
...

 

[laymanB]

As far as the twin paradox is concerned, would it be correct to state the problem and solution as such?

1. The events that we are defining to compare differential aging are that of the Earth and space twin originally united as event A, and the reunion of the twins at the same location on Earth as event B.

2. In either of the inertial reference frames (IRF), the Earth twin is not moving through space relative to the spatial components of events A and B, so only the time component of spacetime is changing for the Earth twin.

3. In either of the IRF, the space twin is moving through space relative to the spatial components of events A and B, so both the time and space components are changing relative to the events' spatial location for the space twin.

4. A straight line in Minkowski spacetime is the longest proper time $\tau$, therefore the longest proper time $\tau$ will be measured by the Earth twin, irrespective of which frame does the calculations?

5. If we know the relative velocity, we can then figure the time dilation using the Lorentz factor $$\Delta t' = \frac{\Delta t}{\sqrt{1-\frac{v^2}{c^2}}}$$ to figure the differential aging. Or we can simply compare the proper times $\tau$ of both twins and work out the relative velocity for the trip. And although the time dilation can normally be applied symmetrically where each twin can claim to be the one at rest, only the space twin in our thought experiment is moving through space relative to the spatial components of the defined events, so that twin's age must be less.

Maybe?? (Crossing my fingers)

 

[PeroK]

@laymanB

Only the Earth twin stays in the same IRF throughout. The space twin changes his IRF at the turn around point.

That's the critical difference.

 

[PeterDonis]

The events that we are defining to compare differential aging are that of the Earth and space twin originally united as event A, and the reunion of the twins at the same location on Earth as event B.

Yes.

In either of the inertial reference frames (IRF)

"Either" implies that there are two IRFs. That's not the case; there are three: the Earth frame, the traveling twin's outbound frame, and the traveling twin's inbound frame.

the Earth twin is not moving through space relative to the spatial components of events A and B

This doesn't make sense. Relative motion applies to objects, not events or components of events.

only the time component of spacetime is changing for the Earth twin

There is no unique "time component of spacetime", so this doesn't make sense either.

In either of the IRF, the space twin is moving through space relative to the spatial components of events A and B, so both the time and space components are changing relative to the events' spatial location for the space twin.

This doesn't make sense either. See above.

A straight line in Minkowski spacetime is the longest proper time $\tau$, therefore the longest proper time $\tau$ will be measured by the Earth twin, irrespective of which frame does the calculations?

This is true, but it doesn't follow from your statements 2 and 3, since those don't make sense.

A correct statement would be: the Earth twin is inertial for the entire trip--he feels no acceleration. (We are ignoring the acceleration felt due to being at rest on Earth; I've always thought a proper setting of this thought experiment would have the "Earth" twin floating out in space, at rest relative to Earth but far enough away that he doesn't need to fire rockets to stay at rest relative to Earth during the experiment.) An unaccelerated worldline corresponds to a straight line in Minkowski spacetime. Then the statement of yours quoted just above follows (with one additional clarification, that we are talking about all possible worldlines between the same two events A and B).

 

[laymanB]

I've always thought a proper setting of this thought experiment would have the "Earth" twin floating out in space, at rest relative to Earth but far enough away that he doesn't need to fire rockets to stay at rest relative to Earth during the experiment.) An unaccelerated worldline corresponds to a straight line in Minkowski spacetime. Then the statement of yours quoted just above follows

Thanks Peter. It seems to me that without acceleration, the problem is truly symmetrical. The space twin could claim to be at rest while the Earth recedes away at some relative velocity and then the Earth frame would have to change inertial reference frames to come back. The spacetime diagrams would be mirror images of each other along the time axis when drawn from either frame as the rest frame.

 

[PeterDonis]

without acceleration, the problem is truly symmetrical

In flat spacetime, without acceleration--meaning, without either twin feeling acceleration--there is no way for the twins to meet up again.

The space twin could claim to be at rest while the Earth recedes away at some relative velocity and then the Earth frame would have to change inertial reference frames to come back.

No, that won't work. "Change inertial reference frames" means the Earth twin--meaning the twin just floating out in free space, at rest relative to the Earth--would have to feel acceleration. He doesn't. It's the traveling twin that feels acceleration.

 

[PeroK]

Thanks Peter. It seems to me that without acceleration, the problem is truly symmetrical. The space twin could claim to be at rest while the Earth recedes away at some relative velocity and then the Earth frame would have to change inertial reference frames to come back. The spacetime diagrams would be mirror images of each other along the time axis when drawn from either frame as the rest frame.

If you forget about twins and just use clocks, then you could transfer the reading from a clock on an outbound ship to a clock on an inbound ship. That way you could measure the proper time of the out-and-back journey without acceleration.

 

[laymanB]

In flat spacetime, without acceleration--meaning, without either twin feeling acceleration--there is no way for the twins to meet up again.

Agreed.

No, that won't work. "Change inertial reference frames" means the Earth twin--meaning the twin just floating out in free space, at rest relative to the Earth--would have to feel acceleration. He doesn't. It's the traveling twin that feels acceleration.

I'm sorry Peter, I should have been clearer. I was referring to the standard twin paradox setup without acceleration (or more precisely, the impossible thought experiment where the constant relative velocity is reached instantaneously, the acceleration of turnaround is ignored, and the deceleration back to Earth to compare clocks is instantaneous). I agree that in your modified version, the Earth twin floating in free space at rest with respect to the Earth would not feel an acceleration. Your version would be asymmetric and the space twin would age less.

I meant in the impossible original thought experiment neglecting acceleration, that the problem setup is truly symmetrical.

 

[PeroK]

I meant in the impossible original thought experiment neglecting acceleration, that the problem setup is truly symmetrical.

No it isn't. The traveller changes his/her IRF.

 

[laymanB]

No it isn't. The traveller changes his/her IRF.

Thanks for the responses. Sorry, I still don't see it. The two twins agreed upon a coordinate system and synchronized their clocks to time 0. The "space" twin could consider himself at rest while the Earth and its twin reached an instantaneous relative velocity in the -x direction of the coordinate system until the original target planet reached the origin ($t+\Delta t$,0,0,0) where the "space" twin was at rest. Then the Earth and its twin switch IRF instantaneously, and head in the x direction with the same relative velocity as the outbound leg, before instantaneously coming to rest with respect to the waiting "space" twin. In this scenario, would not the Earth twin be the younger one according to the original setup (not Peter's version)?

 

[PeroK]

Thanks for the responses. Sorry, I still don't see it. The two twins agreed upon a coordinate system and synchronized their clocks to time 0. The "space" twin could consider himself at rest while the Earth and its twin reached an instantaneous relative velocity in the -x direction of the coordinate system until the original target planet reached the origin (t+X,0,0,0) where the "space" twin was at rest. Then the Earth and its twin switch IRF instantaneously, and head in the x direction with the same relative velocity as the outbound leg, before instantaneously coming to rest with respect the waiting "space" twin. In this scenario, would not the Earth twin, be the younger one according to the original setup (not Peter's version)?

I fear we have another digression.

In any case, the original problem setup is clear: the traveller changes IRF.

If you don't know who changed IRF, then you'd have to wait and see. Unless they both changed IRF, one would be older.

But, all this is missing the point. The acceleration, per se, does not influence the outcome.

If the twin paradox achieves anything, it gets you thinking about the importance of reference frames. If you go away thinking it illustrates the important effects of acceleration, then you're missing the point.

 

[PeterDonis]

I was referring to the standard twin paradox setup without acceleration (or more precisely, the impossible thought experiment where the constant relative velocity is reached instantaneously, the acceleration of turnaround is ignored, and the deceleration back to Earth to compare clocks is instantaneous).

The acceleration of turnaround is not ignored in this formulation. It is just idealized to occur instantly. It can't be ignored since it makes the traveling twin's worldline not a straight line; instead it's two straight lines with a "corner" at the turnaround. There is no "corner" in the Earth twin's worldline. That's the asymmetry.

the Earth and its twin switch IRF instantaneously

No, they don't. "Switching IRF" requires a "corner" in the worldline. There is no "corner" in the Earth twin's worldline; the "corner" is in the traveling twin's worldline. See above.

In this scenario, would not the Earth twin be the younger one according to the original setup (not Peter's version)?

The original setup has the "corner" in the traveling twin's worldline, not the Earth twin's worldline. That makes the Earth twin older when they meet up again.

 

[PeterDonis]

It can't be ignored since it makes the traveling twin's worldline not a straight line; instead it's two straight lines with a "corner" at the turnaround. There is no "corner" in the Earth twin's worldline. That's the asymmetry.

To emphasize the frame-independence of this: the three worldline segments--Earth twin's from A to B, traveling twin's from A to turnaround, and traveling twin's from turnaround to B--form a triangle in spacetime. That is true regardless of which frame you pick. Even if you pick a non-inertial frame in which the traveling twin is always at rest, it is still a triangle, with a "corner" at the traveling twin's turnaround and no "corner" anywhere on the Earth twin's worldline between A and B. In other words, the asymmetry is a geometric property of the scenario. You can't change that property by changing frames, any more than you can change which points are the corners of an ordinary triangle in Euclidean geometry by changing coordinates. It's geometry.

 

[laymanB]

Even if you pick a non-inertial frame in which the traveling twin is always at rest

So are you saying that the frame in which the traveling twin see himself at rest during the whole time from event A to B in a non-inertial frame?

 

[laymanB]

If you forget about twins and just use clocks, then you could transfer the reading from a clock on an outbound ship to a clock on an inbound ship. That way you could measure the proper time of the out-and-back journey without acceleration.

I like this. It seems to make it much harder to think of the setup as symmetric.

 

[Ibix]

So are you saying that the frame in which the traveling twin see himself at rest during the whole time from event A to B in a non-inertial frame?

Yes.

 

[PeterDonis]

So are you saying that the frame in which the traveling twin see himself at rest during the whole time from event A to B in a non-inertial frame?

Yes. That should be obvious.

 

[laymanB]

Sorry, this is the only image I could find on Wiki Commons. I realize that it shows the "corner" as rounded off signifying a more realistic acceleration for the turnaround. This would be the spacetime diagram drawn in the Earth twin reference frame, correct? With his worldline from O to B in a straight line, and the traveling twin's worldline going from O to C and C to B? (Sorry to change the conventions we have been using)

So I was envisioning that if the spacetime diagram drawn in the reference frame of the traveling twin who considers himself at rest the entire time, that is image would be symmetric along the ct axis. Obviously not right.

 

[laymanB]

Yes. That should be obvious.

Oh how that I wish it was. I find that most places that teach about the twin paradox make no mention of how to solve it without resorting to acceleration. Including the link you provided in this thread.

http://math.ucr.edu/home/baez/physics/Relativity/SR/TwinParadox/twin_paradox.html

EDIT: In post #27, you did say that the acceleration is not ignored, just idealized.

 

[PeroK]

Sorry, this is the only image I could find on Wiki Commons. I realize that it shows the "corner" as rounded off signifying a more realistic acceleration for the turnaround. This would be the spacetime diagram drawn in the Earth twin reference frame, correct? With his worldline from O to B in a straight line, and the traveling twin's worldline going from O to C and C to B? (Sorry to change the conventions we have been using)

View attachment 216614

So I was envisioning that if the spacetime diagram drawn in the reference frame of the traveling twin who considers himself at rest the entire time, that is image would be symmetric along the ct axis. Obviously not right.

There's a difference between a rest frame and an IRF. In a previous thread I analyzed this problem from the traveller's outbound IRF. In this frame, the Earth moves with constant velocity. On the outward leg, the traveller is at rest in this frame. But, on the homeward leg the traveller is also moving in this frame.

The thing the traveller cannot do is associate their rest frame with a single IRF throughout.