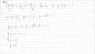Does this line lie in this plane?

[jegues]

Homework Statement

See figure for problem statement. It asks if a given line lies in a given plane.

Homework Equations

The Attempt at a Solution

Okay so first I translated the line into its parametric equations and then I subbed those into the equation of the plane respectively.

After simplifying you'll find that,

$$9t-1 = -1$$

Now my solutions manual states the following,

*NOTE* There is no symbol for not-equivalent in tex, so I'm writing NE

$$9t -1 NE -1$$

Why is this so?

Why not let t = 0, and then -1 = -1 and then all will be well in world, no?

What am I missing?

 

[gabbagabbahey]

*NOTE* There is no symbol for not-equivalent in tex, so I'm writing NE

\neq works

$$9t -1 \neq -1$$

Why is this so?

Why not let t = 0, and then -1 = -1 and then all will be well in world, no?

What am I missing?

Each value of $t$ corresponds to a single point on the line. If the entire line were to lie in the plane, the equation would have to be true for all values of $t$ (all points on the line), not just $t=0$