Destroxia
- 204
- 7
Hello, I've been working through some Digital Signal Processing stuff by myself online, and I saw a system that I wanted to write down as a Linear Algebra Equation. It's a simple delay feedback loop, looks like this:
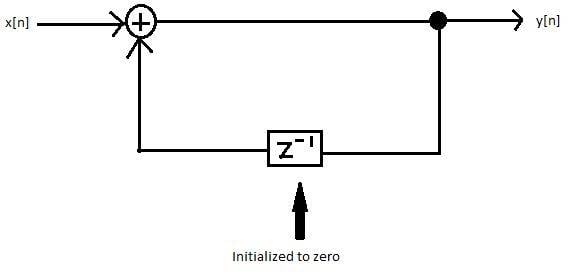
The (+) is an adder that adds 2 signals together, so the signal from x[n] and z^-1 will be added each time until a full signal is formed for the output y[n].
However, on the first run of the loop, z^-1 is initialized to 0, so it's contribution on the first run is zero. (z^-1 will return always return whatever it was last fed, so on the second run it will have whatever came from x[n] the first time and spit that out)So we can model this system as: $$ y[n]=x[n]+ D\lbrace y[n] \rbrace=x[n]+y[n-1], \space \space \space \space \space \space y[0]=x[0]=1$$
Where: $$\space x[n], \space y[n] \space \in \space \mathbb{C}^{N}$$
and D is a size NxN linear operator matrix which represents z^-1, which acts like so: ## D[{x[n]}]= x[n-1] ##
If you want, you can generalize the system for more delay: $$ y[n]=x[n]+ D_{N}\lbrace y[n] \rbrace=x[n]+y[n-N], \space \space \space \space \space \space y[0]=x[0]=1$$
Now imagine we have an input x[n] of dimension 4 that is simply a pulse:
$$
x =
\left[ {\begin{array}{c}
1\\
0\\
0\\
0\\
\end{array} } \right]
$$
If we push this input into the system, with say a delay of Z^-2, we should get a pulse every 2 loops, so the output would look like so:
$$
y =
\left[ {\begin{array}{c}
1\\
0\\
1\\
0\\
\end{array} } \right]
$$
My issue is, when I try to model this with a linear algebra equation, there is recursion, and I can't seem to get a closed form due to an non-invertible matrix. I was looking at recurrence relations on wikipedia to try to solve my issue, but I guess I just don't understand them yet.
My process for modeling this in Linear Algebra has gone like so:
$$ y = x + Dy $$
$$ y - Dy = x$$
$$ (I - D)y = x $$
$$ I -D =
\left[ {\begin{array}{cccc}
1 & 0 & 0 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & 1 & 0\\
0 & 0 & 0 & 1\\
\end{array} } \right]
-
\left[ {\begin{array}{cccc}
0 & 0 & 0 & 1\\
1 & 0 & 0 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & 1 & 0\\
\end{array} } \right]
=
\left[ {\begin{array}{cccc}
1 & 0 & 0 & -1\\
-1 & 1 & 0 & 0\\
0 & -1 & 1 & 0\\
0 & 0 & -1 & 1\\
\end{array} } \right] )
$$
This matrix appears to be uninvertible, but I should be able to somehow create a closed form for this system... I just need to be pointed in the right direction.
(I apologize if this is the wrong board for this, but this is more of a linear algebra question than a signal processing question, as I understand the signal processing part.)
The (+) is an adder that adds 2 signals together, so the signal from x[n] and z^-1 will be added each time until a full signal is formed for the output y[n].
However, on the first run of the loop, z^-1 is initialized to 0, so it's contribution on the first run is zero. (z^-1 will return always return whatever it was last fed, so on the second run it will have whatever came from x[n] the first time and spit that out)So we can model this system as: $$ y[n]=x[n]+ D\lbrace y[n] \rbrace=x[n]+y[n-1], \space \space \space \space \space \space y[0]=x[0]=1$$
Where: $$\space x[n], \space y[n] \space \in \space \mathbb{C}^{N}$$
and D is a size NxN linear operator matrix which represents z^-1, which acts like so: ## D[{x[n]}]= x[n-1] ##
If you want, you can generalize the system for more delay: $$ y[n]=x[n]+ D_{N}\lbrace y[n] \rbrace=x[n]+y[n-N], \space \space \space \space \space \space y[0]=x[0]=1$$
Now imagine we have an input x[n] of dimension 4 that is simply a pulse:
$$
x =
\left[ {\begin{array}{c}
1\\
0\\
0\\
0\\
\end{array} } \right]
$$
If we push this input into the system, with say a delay of Z^-2, we should get a pulse every 2 loops, so the output would look like so:
$$
y =
\left[ {\begin{array}{c}
1\\
0\\
1\\
0\\
\end{array} } \right]
$$
My issue is, when I try to model this with a linear algebra equation, there is recursion, and I can't seem to get a closed form due to an non-invertible matrix. I was looking at recurrence relations on wikipedia to try to solve my issue, but I guess I just don't understand them yet.
My process for modeling this in Linear Algebra has gone like so:
$$ y = x + Dy $$
$$ y - Dy = x$$
$$ (I - D)y = x $$
$$ I -D =
\left[ {\begin{array}{cccc}
1 & 0 & 0 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & 1 & 0\\
0 & 0 & 0 & 1\\
\end{array} } \right]
-
\left[ {\begin{array}{cccc}
0 & 0 & 0 & 1\\
1 & 0 & 0 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & 1 & 0\\
\end{array} } \right]
=
\left[ {\begin{array}{cccc}
1 & 0 & 0 & -1\\
-1 & 1 & 0 & 0\\
0 & -1 & 1 & 0\\
0 & 0 & -1 & 1\\
\end{array} } \right] )
$$
This matrix appears to be uninvertible, but I should be able to somehow create a closed form for this system... I just need to be pointed in the right direction.
(I apologize if this is the wrong board for this, but this is more of a linear algebra question than a signal processing question, as I understand the signal processing part.)