- #1
andyrk
- 658
- 5
Homework Statement
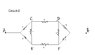
Calculate the effective resistances between P and Q in circuit-1 and A and B in circuits 2 and 3 in each of the following circuit diagrams.
In circuits 2 and 3 the resistance R has the value 1Ω.
2. The attempt at a solution
1. Why does the AB branch get removed in circuit-1 when we simplify the circuit further? Is it because A and B are points at equal potential (equipotential)? But then why are A and B equipotential points?
2. Why do the CE and DF branches get removed in circuit-2 when we simplify the circuit further? It s because points C,E and D,F are equipotential pair of points. But why are they equipotential points?
3. Circuit-3 simplifies to circuit-2 with CD resistance being 10/9Ω and EF resistance being 2/3Ω. All the rest of the resistances are 1Ω. But how does this happen? How does it get simplified to this?