Aubiefan
- 16
- 0
I am having a lot of difficulty with this problem:
Consider a frictionless track as shown in Figure P6.48. A block of mass m1 = 4.20 kg is released from A. It makes a head on elastic collision at B with a block of mass m2 = 10.5 kg that is initially at rest. Calculate the maximum height to which m1 rises after the collision.
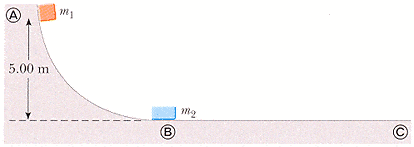
My plan was to use (KE+PE)i=(KE+PE)f, somehow.
I know that at the time of release block A has 205.8 J of potential energy, from PE=mgy, but I need the final velocity in order to use the conservation equation.
I found the velocity before the collision using (delta y)=.5(Vyo+Vy)t, and got 9.9m/s for Block A, B is at rest.
Then I tried to figure out the velocity after the collision, using (m1v1+m2v2)i = (m1v1+m2v2)f
I had (4.2 x 9.9)= (m1v1+m2v2)f, so m2v2f=41.58-m1v1, and that is where I seem to be stuck, I can't figure out how to carry on or if I am even right up to this point. Any tips are EXTREMELY appreciated!
Consider a frictionless track as shown in Figure P6.48. A block of mass m1 = 4.20 kg is released from A. It makes a head on elastic collision at B with a block of mass m2 = 10.5 kg that is initially at rest. Calculate the maximum height to which m1 rises after the collision.
My plan was to use (KE+PE)i=(KE+PE)f, somehow.
I know that at the time of release block A has 205.8 J of potential energy, from PE=mgy, but I need the final velocity in order to use the conservation equation.
I found the velocity before the collision using (delta y)=.5(Vyo+Vy)t, and got 9.9m/s for Block A, B is at rest.
Then I tried to figure out the velocity after the collision, using (m1v1+m2v2)i = (m1v1+m2v2)f
I had (4.2 x 9.9)= (m1v1+m2v2)f, so m2v2f=41.58-m1v1, and that is where I seem to be stuck, I can't figure out how to carry on or if I am even right up to this point. Any tips are EXTREMELY appreciated!