Elastic Spring / Simple Pendulum Lowest Point

[ln(]

Homework Statement

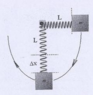
A perfectly elastic spring swings in a vertical plane as a simple pendulum with a mass m suspended at the bottom of the spring. The force constant for this spring is $k$ and the unstretched length is $L$. The spring is carefully held in the horizontal position so that the spring is unstretched when released. The spring then swings through the vertical position. What is the increase in the length of the spring when the spring passes through the vertical position?

Homework Equations

$E_i = E_f$ (conservation of mechanical energy)
$\frac{mv^2}{r} = F_c$

The Attempt at a Solution

It says that this is a simple pendulum, and doesn't specify any block width, so I'll assume that the mass is a point mass. I'll have $\Delta x := x$ to make it easier to type.
I know that mechanical energy is conserved so $mg(L + x) = \frac{1}{2}mv^2 + \frac{1}{2}kx^2$ at the lowest point.
I need to get rid of $v$ in my equation and the only other thing I can think of is centripetal force. I question if I can actually use this since I don't think this system moves with a constant distance to the pivot; I think I would need to use the radius of curvature for the parabola (?) that results. I'm not sure so I have just tried to use centripetal force directly: $kx - mg = \frac{mv^2}{L+x}$. However, once I get this, combining everything gives me a very unwieldy quadratic that doesn't correspond to any of the given answer choices.

 

[mfb]

I question if I can actually use this since I don't think this system moves with a constant distance to the pivot

You don't even know if the motion is purely horizontal. If it is (I don't think this is physically possible), then the extension reaches its maximum there, but that still doesn't tell you what the acceleration is.

There is one answer choice that works. And you don't even have to solve equations for it.

 

[ln(]

You don't even know if the motion is purely horizontal. If it is (I don't think this is physically possible), then the extension reaches its maximum there, but that still doesn't tell you what the acceleration is.

There is one answer choice that works. And you don't even have to solve equations for it.

I still don't see how to do it. Or do you mean that there isn't enough info?

 

[mfb]

Or do you mean that there isn't enough info?

Exactly.

 

[Orodruin]

Exactly.

The equations of motion are two second order differential equations and there are four initial conditions. The system is perfectly well determined and for any set of the parameters you can easily find the value of the extension at the bottom numerically. Based on what I have seen by doing this, it is not what the problem authors had in mind though ...

 

[BvU]

The equations of motion are two second order differential equations and there are four initial conditions. The system is perfectly well determined and for any set of the parameters you can easily find the value of the extension at the bottom numerically. Based on what I have seen by doing this, it is not what the problem authors had in mind though ...

I was wondering: is the extension independent of $L$ (which is not given...) ?

 

[Orodruin]

I was wondering: is the extension independent of $L$ (which is not given...) ?

No, in general it will depend on L. From the problem it seems that L is given as it is mentioned in the statement. However, this just means all the options are wrong.

The general form of the solution should relate x, L, m, g, and k. Those are five variables with three basic physical dimensions. You can therefore construct two dimensionless combinations:
$$
\pi_1 = \frac{kx}{mg}, \quad \pi_2 = \frac{kL}{mg}.
$$
By Buckingham’s pi theorem, this implies that
$$
\pi_1 = f(\pi_2) \quad \Longrightarrow \quad
x = \frac{mg}{k} f(kL/mg),
$$
where $f$ is some dimensionless function. This is the closest you can get without looking at the equations of motion.

 

[Orodruin]

Assuming that I entered everything into Mathematica correctly, this is what I get numerically for $f(\pi_2)$ in the range 0 to 10, clearly a non-trivial behaviour:

 

[haruspex]

You don't even know if the motion is purely horizontal.

I agree it would not be, but the given diagram seems to suppose that it is. On that basis, I get
3mg(L+x)=kLx+2kx².
This makes x depend on L, as ln( found.

To eliminate L from the equation we need x=3mg/k, but that leaves the rest of the equation as x=3mg/2k, so there is no consistent solution without L. These would be the limiting solutions as L tends to infinity and 0 respectively, but still with the invalid assumption of horizontal motion.
I guess large L would be the same as small x, and this would also mean very little vertical motion, so option d) may be ok as a small x approximation.

I tried a few simple algebraic errors, but could not reproduce any of the given answers.

 

[Orodruin]

I agree it would not be, but the given diagram seems to suppose that it is.

I think we already concluded that the problem constructor has made a logical blooper somewhere along the way. For definiteness, these are the solutions I get for $\pi_2 = 0.01$, i.e., essentially in the small $L$ limit ($\theta$ being the coordinate starting at $\pi/2$):

Clearly $\dot x \neq 0$ when $\theta = 0$, indicating that the motion indeed is not horizontal at $\theta = 0$. Instead, the elongation in $x$ has already passed its largest value and the mass is again on its way up.

 

[haruspex]

in the small L limit

Yes, but I am suggesting the large L limit (small x).

 

[Orodruin]

It turns out I indeed had a typo stemming from when I started using units of $m$, $k$, and $g$ instead of $m$, $L$, and $g$ ... These are the corrected plots:

Small L regime (L = 0.01)

Maximal x around 2mg/k. This makes sense, it is essentially dropping the mass attached to a spring and solving mgx = kx^2/2.

$f(\pi_2)$

Large L regime (L = 100)

There are some wiggles on the $x$ solution due to the oscillations around the force equilibrium, but their amplitude is small relative to the amplitude of the force equilibrium itself. Indeed, the maximal extension is $x \simeq 3mg/k$ at $\theta \simeq 0$.

 

[mfb]

The equations of motion are two second order differential equations and there are four initial conditions. The system is perfectly well determined and for any set of the parameters you can easily find the value of the extension at the bottom numerically. Based on what I have seen by doing this, it is not what the problem authors had in mind though ...

Sure, it is well-determined, but without knowing more about L we cannot say what happens (as your simulations confirm) - unless we express it as function of L, but none of the answers does this.

Axis/graph labels would make it easier to understand what you are plotting, by the way.

 

[haruspex]

unless we express it as function of L, but none of the answers does this.

Sure, but that does not make e) the answer. The answer becomes "none of the above".

 

[Orodruin]

but none of the answers does this.

Indeed. I think we are all old enough to have found errors in problem formulations before? I would tend to believe @haruspex in that the problem constructor imagined the large L regime. Of course, this does not make the problem correct.

Axis/graph labels would make it easier to understand what you are plotting, by the way.

- Labels?! We don't need to show you any stinkin' labels!


Obviously, this was a quick mashup and I think it is fairly self-explanatory based on the written descriptions. Anyway, the solutions are the generalised coordinates (in units of $mg/k$ and $1$, respectively) as a function of time in units of $\sqrt{m/k}$. The plot of $f(\pi_2)$ is just a plot of a dimensionless function of a dimensionless variable.