lawk
- 3
- 0
Homework Statement
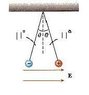
Two small spheres, each of mass 8.00 g , are suspended by light strings 15.0 cm in length (see figure). A uniform electric field is applied in the x direction. The spheres have charges equal to -6*10^-8 and 6*10^-8 Determine the electric field that enables the spheres to be in equilibrium at an angle of 11 degree.
Homework Equations
ke = 8.99*10^9
gravity= 9.8 m/s^2
ke(q1*q2)/r^2 ?
The Attempt at a Solution
I don't know how to approach the problem.
I don't know how gravity is affecting the problem.
Can someone guide me through the problem?
What should I do in order to get the answer?