Electric Circuit Connected to Ground

[Ricky2357]

Homework Statement

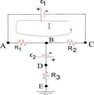
Given the attached scheme, if R_{1}=R_{2}=R_{3}=10 Ω and \epsilon_{1}=20 V , \epsilon_{2}=10 V determine the potentials at the points A,B,C,D,E. The sources of emf have no internal resistance.

Homework Equations

My question is: Why is it that no current exists along the branch BE? If one made this particular apparatus I am convinced he would observe no current. But in theory, why does this happen? Shouldn't the source of emf \epsilon_{2} produce some current?
And even if \epsilon_{2} , R_{3} did not exist, why would the current ''choose'' to move around the loop instead of going towards the ground?

The Attempt at a Solution

Assuming no current exists at the branch BE, we assign zero potential at points D,E. Because of \epsilon_{2} we have V_{B}=-10 V.
Due to our assumption, current exists only within the loop. We easily find its value:
I=1 A. Using the mathematical expression of Ohm's law we may now easily obtain the wanted potentials:
V_{A}=0 V , V_{C}=-20 V

 

[kamerling]

There is no return path for the current. If there was a current from B to E, the electrons would either pile up somewhere in the loop or the loop would get depleted of electrons.

What would happen if you connected the loop to point B is that a current would flow for a very short time, until a very small negative charge is distributed around the loop. This charge would prevent any further electrons going through the loop through BE. Their electric field would be the source of the overall negative potential of the loop.
(It's much easier to forget about this and just go with: "no closed loop - no current")