Pranav-Arora said:
The strength of electric field decreases and becomes half. Surprising? I am not sure, I am not good at interpreting the final results, can you show me why this is interesting? :)
Thanks a lot Simon Bridge.

What your result is telling you is that half the electric field close to the surface is due to the charge in the very small region close by.
You don't think that's interesting?
Admittedly, all that charge was very close to the point of interest.
At the risk of confusing you: there are several ways of thinking about this problem.
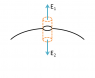
If you treat any point at r=R to be infinitesimally outside the sphere, for example, then Gauss' law will have you treat all the charge as at the centroid.
For a small hole, the centroid will be close to the center of the equivalent complete sphere. What does that do to your calculation?
If you treat the hole diameter d as removing a disk from the surface - d<<R means that the removed section is approximately flat.
The field at the center of the hole would be the field, there, due to the entire sphere, minus the field at the center of a flat disk.
The field in the center of a flat disk is...
You could say that the center of the hole is at distance ##C=R\cos\alpha = \sqrt{R^2-d^24}## ##\alpha## being half the apex angle of a cone with the hole as it's base, point at the origin. In which case, C<R so there is no charge inside, so the field is zero.
All these ways appear to contradict the "correct" answer. But they each make some kind of assumption...
The exercises you are being given are not arbitrary - they are supposed to teach you stuff beyond how to do the calculation.
But the prof is probably happy that you could do the calculation, but, especially in exams, it can be helpful (i.e. to the final grade) to write a short bit in more regular language about what the answer is telling you.