Electric Field from its Potential of a Half Circle along its Z axis

[AndresPB]

Homework Statement

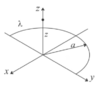
Find the Electric Potential Energy of half a circle charged with a Linear Charge Density: "Lambda" along its z axis. After that, find the Electric Field "E" deriving its potential energy.

Relevant Equations

Potential Energy dV = (1/(4*Pi*Epsilon_0))*(dQ/|r-r'|)
Electric Field E = - ∇ V

So I figured out the potential is: dV = (1/(4*Pi*Epsilon_0))*[λ dl/sqrt(z^2+a^2)]
.
From that expression: We can figure out that since its half a ring we have to integrate from 0 to pi*a, so we would get:

V = (1/(4*Pi*Epsilon_0))*[λ {pi*a]/sqrt(z^2+a^2)]

In that expression: a = sqrt(x^2+y^2)

What I am having trouble is getting the electric field from this expression. When I do ∇ V, I am getting three components for my electric field in the (x,y,z), directions. But when I analyze the problem. It is clear to me that there is not a "y" component, as there is simetry along this axis. What shall I do?

The answer I am getting at the moment is this ("L" in this case is: (1/(4*Pi*Epsilon_0))*[λ {pi}]):

 

[mjc123]

It looks like you are using x and y for different things. There is the equation of the semicircle: x² + y² = a². Then there are the coordinates of a point in space (x, y, z), for which you want to find the potential and its derivative. But you can't use the same x and y for both, and try to differentiate by them. You have to label them differently. For example, you could calculate the potential by
V = ∫λadΦ/(4πε₀R) where R² = (x-acosφ)² + (y-asinφ)² + z²
Differentiate, and take x = y = 0 along the z axis.

 

[kuruman]

You can get the electric field on the $z$-axis from the electric potential $V(z)$. Note that all elements $dq$ on the ring are at the same distance from the point of interest on the $z$-axis. Would $V(z)$ be any different if you squeezed all the charge on the ring into a single point charge in the $xy$ plane at distance $a$ from the origin ?