Electric field in coaxial cable

AI Thread Summary
In a coaxial cable, the electric field is primarily axial within the conductors, with a perpendicular component between them, influenced by surface charges. The discussion highlights a contradiction in the propagation of TEM waves, where Ohm's law suggests a current flow in the same direction as the electric field. In an ideal scenario with infinite conductivity, the propagation is purely TEM, implying no longitudinal electric field component. The question arises about the force that drives charge flow in this ideal case. Understanding these dynamics is crucial for comprehending wave propagation in coaxial cables.
oocelik
Messages
2
Reaction score
0
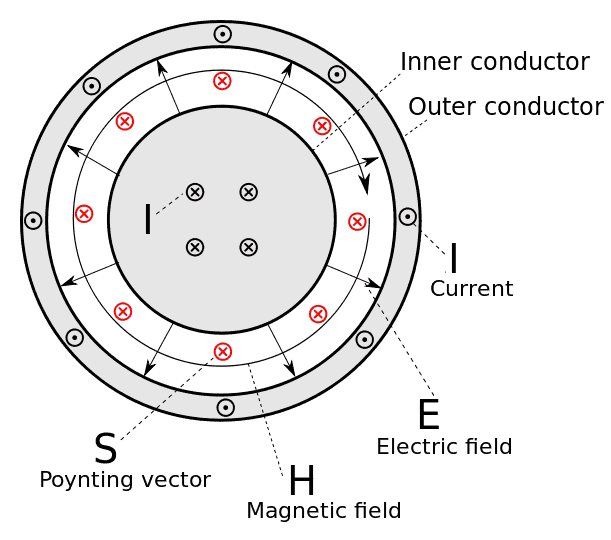
Every physics books show that wave prograpation in coxial cable is TEM wave, like in the picture. But we know that J=σ E from ohms law, which says current in same direction with E field, which is not the case here. What do you think the reason is ?

UzJYy.png
 
Physics news on Phys.org
Hello Dale,

Thank you for the reply. But I am talking about the ideal case where the cable has infinite conductivity and progpagation is pure TEM wave, which makes it sure that there is no "longitudinal" (i.e Ez=0) along the cable by definition. In this case, what force acts on the charges to flow down the cable ?
 

Thread 'How to picture the vector potential?'

Susskind (in The Theoretical Minimum, volume 1, pages 203-205) writes the Lagrangian for the magnetic field as ##L=\frac m 2(\dot x^2+\dot y^2 + \dot z^2)+ \frac e c (\dot x A_x +\dot y A_y +\dot z A_z)## and then calculates ##\dot p_x =ma_x + \frac e c \frac d {dt} A_x=ma_x + \frac e c(\frac {\partial A_x} {\partial x}\dot x + \frac {\partial A_x} {\partial y}\dot y + \frac {\partial A_x} {\partial z}\dot z)##. I have problems with the last step. I might have written ##\frac {dA_x} {dt}...
View full post »
Thread 'Griffith, Electrodynamics, 4th Edition, Example 4.8. (Second part)'

Thread 'Griffith, Electrodynamics, 4th Edition, Example 4.8. (Second part)'

I am reading the Griffith, Electrodynamics book, 4th edition, Example 4.8. I want to understand some issues more correctly. It's a little bit difficult to understand now. > Example 4.8. Suppose the entire region below the plane ##z=0## in Fig. 4.28 is filled with uniform linear dielectric material of susceptibility ##\chi_e##. Calculate the force on a point charge ##q## situated a distance ##d## above the origin. In the page 196, in the first paragraph, the author argues as follows ...
View full post »

Similar threads

A Voltage and current waves in a transmission line
Replies
4
Views
3K
Displacement current in coaxial cables
Replies
7
Views
5K
Could a coaxial cable be used for electric current instead of radio signals?
Replies
9
Views
4K
I Do electron density waves accompany EM waves in coaxial cables?
Replies
5
Views
155
Doubts on Ampère's Law and Coaxial Cables
Replies
1
Views
2K
Understanding the Coaxial Inductor: A Study of its Electric and Magnetic Fields
Replies
1
Views
2K
A Why are only TM waves allowed in this geometry? (Planar interface)
Replies
0
Views
999
Maxwell's equations for TEM mode
Replies
2
Views
1K
B Electric Field Created by 2 Infinite Plates
Replies
1
Views
1K
Coaxial cables and displacement current
Replies
1
Views
2K

Hot Threads

Recent Insights

Back
Top