preachingpirate24
- 15
- 2
Let's say I place a positive point charge inside a hollow conducting sphere. If we take a Gaussian surface through the material of the conductor, we know the field inside the material of the conductor is 0, which implies that there is a -ve charge on the inner wall to make the net enclosed charge 0 and a +ve charge on its outer wall. If I remove some electrons from the sphere, my textbook tells me that the +ve charge on the outer surface increases. Does this mean that the Electric Field inside the conductor is not equal to 0?
If it still is equal to 0, can someone please help me understand why? When I remove some negative charge from the conducting sphere's material, the positive charge on its outer surface becomes greater in magnitude, which to me implies that there is an Electric Field inside the conductor.

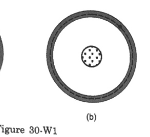

I think I could also be misinterpreting the answer, and the author could be trying to say that the field inside the conductor was 0 before the extra charge was added to it, but then again, the author has stated that there can be no electric field inside a conductor in electrostatics. I understood why that statement is true, but when I add extra charges, I'm really not sure.
Thanks a lot for taking time to help :)
If it still is equal to 0, can someone please help me understand why? When I remove some negative charge from the conducting sphere's material, the positive charge on its outer surface becomes greater in magnitude, which to me implies that there is an Electric Field inside the conductor.
I think I could also be misinterpreting the answer, and the author could be trying to say that the field inside the conductor was 0 before the extra charge was added to it, but then again, the author has stated that there can be no electric field inside a conductor in electrostatics. I understood why that statement is true, but when I add extra charges, I'm really not sure.
Thanks a lot for taking time to help :)