Electric Field Lines, Misconception

[Dweirdo]

Homework Statement

This is a question I read in an article that discusses about misconception of physics among students.
they only provided the question and some of the wrong principles students suggested.

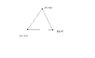
Three Points , located on the vertices(vertexes) of an equilateral triangle and have potentials 0V, 50 V ,-25V as in the figure I attached to this thread.
The students were asked to sketch electric field lines and equipotential surfaces.

Homework Equations

E=V/d
Electric field line's starting point should be either a charge or infinity.
Electric field line's ending point should be either a charge or infinity.

the misconception was that students sketched electric field lines from one point to another as if there were charges there.

The Attempt at a Solution

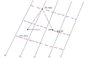
First, I assumed they are apart distance d from each other.
then I divided the question into 3 two-pairs and found the electrical field that should be in a specific direction to satisfy this voltage difference.

e.g
the pair P2 -P1 has potential difference of 50V thus I can assume there is an electric field in the direction from P2 to P1 with magnitude of 50/d (but not starting from point P2, it starts from infinity ,just the direction is... you could say 30 degrees wit the vertical.)
then I summed all the components to find the direction of the "net Electric Field" which happens to be 19.1 degrees(if I'm not mistaken) to the left of the vertical as shown in the second diagram,and the direction is independent of d.

and about the equipotential surfaces,
IMO they are perpendicular to the electric field lines but they are not really surfaces :S just lines, and I'm not sure if it's OK ( they are infinite so I can say the are surfaces ??).

anyway,any suggestions and help is appreciated, I've never been that in-secure in a physics question.


Thank You,
Dw

 

[kuruman]

I suppose it is understood that the electric field is uniform in the region, otherwise the problem would be impossible. If that is the case, I would write the potential in that region of space as

φ(x,y) = C₁x + C₂y + C₃ where all the C's are constants.

The Electric field vector then would be (-C₁, -C₂)

To find these constants, attach coordinates to each point and write the potential. For example, if you put the origin at the leftmost charge, you get

φ(0,0) = -C₃ = -25 V
Do the same with the other three vertices and you will three equations and three unknowns, C₁, C₂ and C₃ (you already know C₃). Solve and get the electric field vector. It will be in terms of the side of the equilateral triangle, but that's just a scaling factor that doesn't change the direction of the field lines relative to the triangle.

 

[Dweirdo]

Hi kuruman!
Thank you for the reply.
They haven't specified in the question that the electric field is uniform in the region,but I assume it's uniform otherwise you are right and problem would be impossible.

With your solution I get the same angle as in my solution!
But the magnitude of the electric field is different.
You solution is right and mine is wrong,i've ended up adding the contribution to x twice and thus making it wrong, but I wonder how I've received the same angle..

I like your solution,Thank You very much for your help!
btw the equipotential surfaces are OK,right?

 

[kuruman]

I am not sure how you ended up adding the contribution to x twice, but not to y and still get the angle right. If the field is E = - (C₁, C₂) then E = - (2C₁, C₂) would give a different angle, but E = - 2(C₁, C₂) would not.

The equipotentials in this case are lines perpendicular to the electric field lines. You can check if they are correct by finding the equation for one of them and plugging in different values for x and y.

 

[Dweirdo]

When I first tried to solve it, I hadn't used your technique,I've explained mine in the first post of this thread,which is conceptually wrong , but logically(then..) was alright.
I've ended up adding all the contributions to the x direction and to the y direction instead of using it just once.
but still I've received the right angle(19.1 as in the first post).. kinda weird, but nvm.

thank You :)