You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Electric field lines of a sphere in a uniform electric field
- Thread starter sergiokapone
- Start date
AI Thread Summary
The discussion revolves around drawing electric field lines of a sphere in a uniform electric field using LaTeX/TikZ, focusing on equations in polar coordinates. Participants clarify that the sphere is a dielectric, not a conductor, which leads to a surface charge distribution due to polarization. The electric field inside the sphere is uniform, represented by parallel lines, while the charge distribution on the surface is influenced by the surrounding medium's susceptibility. The equation for the field inside the sphere is provided, highlighting the relationship between the dielectric constants of the materials involved. The conversation emphasizes the importance of understanding the physical properties of the sphere to accurately depict the electric field lines.
Physics news on Phys.org
- 42,705
- 10,459
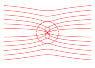
Is this an uncharged conducting sphere? If so, why the field lines inside it, and what direction should the field lines be at the external surface?sergiokapone said:I need to draw electric field lines of sphere in uniform electric field with LaTeX/TikZ. Can anyone show me equation of field lines in polar coordinates?
View attachment 216702
sergiokapone
- 306
- 17
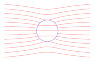
Is the uncharged dielectric sphere. I found some equation
##r = \frac{k - \sin\phi}{E_0\sin\phi}## and plot the lines:
I get
##r = \frac{k - \sin\phi}{E_0\sin\phi}## and plot the lines:
Code:
\begin{tikzpicture}
\clip(-4,-3) rectangle (4,3);
\draw[red] (-4,0) -- (4,0);
\foreach \i in {0,0.5,...,3} {
\draw [thick, color=red, domain=0.05:3.1, samples=200, smooth]
plot (xy polar cs:angle=\x r, radius={ (\i-sin(\x r))/(1*sin(\x r)) });
\draw [thick, color=red, domain=0.05:3.1, samples=200, smooth]
plot (xy polar cs:angle=\x r, radius={ (-\i+sin(\x r))/(1*sin(\x r)) });
}
\fill[white, draw=blue] (0,0) circle (1);
\end{tikzpicture}I get
Attachments
- 42,705
- 10,459
Ok, so it is not a conductor. Looks reasonable, except that I am not sure what the figure of eight inside the sphere represents, or what the field lines are doing there.
sergiokapone
- 306
- 17
haruspex said:that I am not sure what the figure of eight inside the sphere represents, or what the field lines are doing there.
I am also not sure, but the nubber 8 inside is the sequence of eqution.
Last edited:
- 42,705
- 10,459
But... the same equation would not apply inside, would it?sergiokapone said:I am also not sure, but the nubber 8 inside is the sequence of eqution.
- 42,705
- 10,459
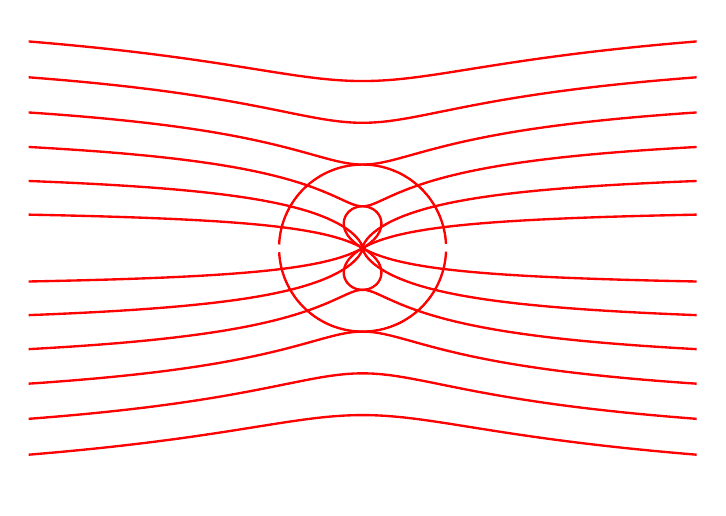
What is the basis for making them parallel inside? Surely those would be distorted by what is going on outside. There is a symmetry here.sergiokapone said:Yes, the same equation would not apply inside. For lines inside I just draw series of parallel lines.
View attachment 216839
sergiokapone
- 306
- 17
Parallel lines inside is because fileld inside sphere (as well as for every "ellipsoid-like" body) is uniform. It uniform because charge distribution around surface is ##\sigma \propto \cos\phi##. Such distribution governing by boundary conditions and supperppsition of external uniform field and dipole field of sphere.
Last edited:
- 42,705
- 10,459
You still have not clearly specified the problem. You have explained that the sphere contains dielectric material, but why should there be a surface charge as you describe? If it is a conductor there is no field inside; if an insulator why should there be a surface charge distribution?sergiokapone said:Parallel lines inside is because fileld inside sphere (as well as for every "ellipsoid-like" body) is uniform. It uniform because charge distribution around surface is ##\sigma \propto \cos\phi##. Such distribution governing by boundary conditions and supperppsition of external uniform field and dipole field of sphere.
Or maybe I am just out of my depth.
sergiokapone
- 306
- 17
Oh, sorry I forgetting to say, the dielectric sphere has the susceptibility ##\epsilon_2## differ from susceptibility of media ##\epsilon_1##, thus there is associated charges on the sphere (due to polarization)
##\sigma' = \frac{3}{4\pi} \frac{\epsilon_1 - \epsilon_2}{\epsilon_1 + 2\epsilon_2} \frac{\vec E_0\vec{r}}{R}.##
Of course, if ##\epsilon_2 =\epsilon_1## there is no charges around sphere.
The field inside sphere is ##E =\frac{3\epsilon_2}{\epsilon_2 + 2\epsilon_1}E_0##
##\sigma' = \frac{3}{4\pi} \frac{\epsilon_1 - \epsilon_2}{\epsilon_1 + 2\epsilon_2} \frac{\vec E_0\vec{r}}{R}.##
Of course, if ##\epsilon_2 =\epsilon_1## there is no charges around sphere.
The field inside sphere is ##E =\frac{3\epsilon_2}{\epsilon_2 + 2\epsilon_1}E_0##
Last edited:
Similar threads
- Replies
- 4
- Views
- 3K
- Replies
- 16
- Views
- 3K
- Replies
- 21
- Views
- 2K
- Replies
- 3
- Views
- 2K
- Replies
- 22
- Views
- 2K
- Replies
- 2
- Views
- 849
- Replies
- 25
- Views
- 2K
- Replies
- 3
- Views
- 1K
- Replies
- 73
- Views
- 5K
- Replies
- 10
- Views
- 2K
Hot Threads
-
I Explain Bernoulli at the molecular level?
- Started by user079622
- Replies: 251
- Classical Physics
-
B What is the Correct Reading on the Scale in This Mass/Scale Puzzle?
- Started by DaveC426913
- Replies: 206
- Classical Physics
-
I Topic about physics axioms, theory, laws etc..
- Started by user079622
- Replies: 93
- Classical Physics
-
I Does kinetic friction propel a person walking forward?
- Started by annamal
- Replies: 41
- Classical Physics
-
First law of this universe
- Started by Anti10188
- Replies: 25
- Classical Physics
Recent Insights
-
Insights Thinking Outside The Box Versus Knowing What’s In The Box
- Started by Greg Bernhardt
- Replies: 1
- Other Physics Topics
-
Insights Why Entangled Photon-Polarization Qubits Violate Bell’s Inequality
- Started by Greg Bernhardt
- Replies: 28
- Quantum Interpretations and Foundations
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 11
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 3
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math