pc2-brazil
- 198
- 3
I'm reading a Physics (electricity and magnetism) book for self-study. I tried to do the exercise below, but I'm not getting the correct answer. This is not actually a homework (since it's not part of a course).
I will try to carefully reproduce the steps I took below, so that someone can help identify the mistake.
Thank you in advance.
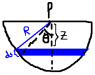
A hemispheric vessel of internal radius R has a total charge q uniformly distributed through its internal surface. Determine the electric field at the center of curvature.
\vec{E} = \int d\vec{E}
E = \frac{kq}{d^2}, where k = \frac{1}{4\pi\epsilon_0}
Electric field produced by a charged ring at a point located at a distance z along its central axis:
E = \frac{kqz}{(z^2 + R^2)^{3/2}}
First, I will call P the point at the center of curvature, and R the radius of the hemisphere.
I will divide the hemisphere into a pile of rings of charge dq and radius r at a distance z from point P. The magnitude of the electric field produced at that point by a ring is:
dE = \frac{kz}{(z^2 + r^2)^{3/2}} dq
The relation between the radius r of the ring, the radius R of the hemisphere and the distance z from the center of the ring to point P is:
R^2 = z^2 + r^2
So, I can substitute it into the expression for dE:
dE = \frac{kz}{R^3} dq
Now I have to express dq in terms of another variable. I will call σ the surface charge density of the hemisphere. So:
dq = \sigma dA
where dA is the area of the ring. Now, I can either (1) express dA in terms of z and express r in terms of z or (2) express dA in terms of r and express z in terms of r. I will choose (2):
dq = \sigma \times 2\pi r dr
Then, the expression for dE becomes:
dE = \frac{kz}{R^3} \times \sigma \times 2\pi r dr
dE = \frac{kz\sigma\times2\pi r}{R^3} dr
In terms of r, z can be written as \sqrt{R^2 - r^2}; so, the above can be rewritten as:
dE = \frac{k\sqrt{R^2 - z^2}\sigma\times2\pi r}{R^3} dr
Now, I want to obtain the electric field produced by all rings at that point. Since the electric fields produced by all rings will be at the same direction and orientation, I will just sum their magnitudes by integrating, with r going from 0 to R:
E = \int_0^R \frac{k\sqrt{R^2 - r^2}\sigma\times2\pi r}{R^3} dr
E =\frac{2\pi k \sigma}{R^3} \int_0^R r\sqrt{R^2 - r^2}\ dr
E = \frac{2\pi k \sigma}{R^3} \left ( -\frac{1}{3}(R^2 - R^2)^{3/2} + \frac{1}{3}(R^2 - 0^2)^{3/2} \right )
E = \frac{2\pi k \sigma}{R^3} \left (\frac{1}{3}R^3 \right )
E = \frac{2\pi k \sigma}{3}
Now, since the surface area of the internal surface of the hemisphere is 2πr² (half the surface area of a sphere), σ is given by:
\sigma = \frac{q}{2\pi R^2}
So, the electric field is:
E = \frac{kq}{3R^2}. Now, I rewrite k as \frac{1}{4\pi\epsilon_0} and get:
E = \frac{q}{12\pi\epsilon_0 R^2}
This is the value I got. But the book's answer is different. It is:
E = \frac{q}{8\pi\epsilon_0 R^2}
What did I get wrong?
Thank you in advance.
I will try to carefully reproduce the steps I took below, so that someone can help identify the mistake.
Thank you in advance.
Homework Statement
A hemispheric vessel of internal radius R has a total charge q uniformly distributed through its internal surface. Determine the electric field at the center of curvature.
Homework Equations
\vec{E} = \int d\vec{E}
E = \frac{kq}{d^2}, where k = \frac{1}{4\pi\epsilon_0}
Electric field produced by a charged ring at a point located at a distance z along its central axis:
E = \frac{kqz}{(z^2 + R^2)^{3/2}}
The Attempt at a Solution
First, I will call P the point at the center of curvature, and R the radius of the hemisphere.
I will divide the hemisphere into a pile of rings of charge dq and radius r at a distance z from point P. The magnitude of the electric field produced at that point by a ring is:
dE = \frac{kz}{(z^2 + r^2)^{3/2}} dq
The relation between the radius r of the ring, the radius R of the hemisphere and the distance z from the center of the ring to point P is:
R^2 = z^2 + r^2
So, I can substitute it into the expression for dE:
dE = \frac{kz}{R^3} dq
Now I have to express dq in terms of another variable. I will call σ the surface charge density of the hemisphere. So:
dq = \sigma dA
where dA is the area of the ring. Now, I can either (1) express dA in terms of z and express r in terms of z or (2) express dA in terms of r and express z in terms of r. I will choose (2):
dq = \sigma \times 2\pi r dr
Then, the expression for dE becomes:
dE = \frac{kz}{R^3} \times \sigma \times 2\pi r dr
dE = \frac{kz\sigma\times2\pi r}{R^3} dr
In terms of r, z can be written as \sqrt{R^2 - r^2}; so, the above can be rewritten as:
dE = \frac{k\sqrt{R^2 - z^2}\sigma\times2\pi r}{R^3} dr
Now, I want to obtain the electric field produced by all rings at that point. Since the electric fields produced by all rings will be at the same direction and orientation, I will just sum their magnitudes by integrating, with r going from 0 to R:
E = \int_0^R \frac{k\sqrt{R^2 - r^2}\sigma\times2\pi r}{R^3} dr
E =\frac{2\pi k \sigma}{R^3} \int_0^R r\sqrt{R^2 - r^2}\ dr
E = \frac{2\pi k \sigma}{R^3} \left ( -\frac{1}{3}(R^2 - R^2)^{3/2} + \frac{1}{3}(R^2 - 0^2)^{3/2} \right )
E = \frac{2\pi k \sigma}{R^3} \left (\frac{1}{3}R^3 \right )
E = \frac{2\pi k \sigma}{3}
Now, since the surface area of the internal surface of the hemisphere is 2πr² (half the surface area of a sphere), σ is given by:
\sigma = \frac{q}{2\pi R^2}
So, the electric field is:
E = \frac{kq}{3R^2}. Now, I rewrite k as \frac{1}{4\pi\epsilon_0} and get:
E = \frac{q}{12\pi\epsilon_0 R^2}
This is the value I got. But the book's answer is different. It is:
E = \frac{q}{8\pi\epsilon_0 R^2}
What did I get wrong?
Thank you in advance.