Electric Field of two line charges

[badluckmath]

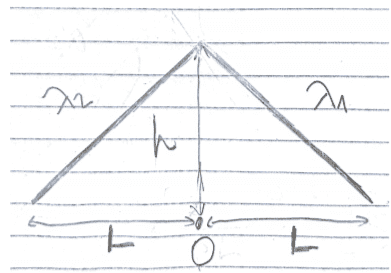
Homework Statement

Find the Electrical Field on the O point

Relevant Equations

$dl = dx\sqrt{1+(\frac{dy}{dx})^{2}}$

I'm trying to solve this, but i don't really know how to start this problem. There are two line charges and i must find the E. Field on the center.

 

[kuruman]

Start with the general expression for the electric field due to a semi-infinite finite line of charge. You may have to look it up or derive it. Then use superposition.

 

[badluckmath]

Start with the general expression for the electric field due to a semi-infinite line of charge. You may have to look it up or derive it. Then use superposition.

Yeah, my confusion is what to do about the inclined wire.

 

[kuruman]

What inclined wire? If I interpret your drawing correctly you have two wires forming a right angle and you want the electric field at distance $h$ from the corner on the 45^o line between the wires. Find the contribution at that point for one wire, then do the same for the second wire. The second wire should be easy because the magnitude will be the same and you will not have to do any more integrals.

On edit: Oops! I just realized that you have wire segments not semi-infinite wires. That should only change the upper limit of integration. Also, it might be easier to do the field components if you rotated the angle so that one wire segment is horizontal and the other vertical like coordinate axes.