Nivlac2425
- 53
- 0
Homework Statement
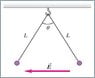
Two tiny spheres of mass m = 7.90 mg carry charges of equal magnitude, 72.0 nC, but opposite sign. They are tied to the same ceiling hook by light strings of length 0.530 m. When a horizontal uniform electric field E that is directed to the left is turned on, the spheres hang at rest with the angle θ between the strings equal to 50.0 degrees in the following figure.
What is the magnitude of E?
Homework Equations
qE = F
The Attempt at a Solution
I know that I need the total force acting on a sphere in order to calculate the electric field strength. I just can't seem to solve for that force.
Does the attraction force of the oppositely charged spheres need to be accounted for as well? Or is the angle separation only caused by the electric field force?
Thanks for helping me out here!
Attachments
Last edited: