Zanker
- 2
- 0
Homework Statement
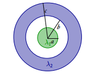
Consider an infinitely long solid cylinder of uniform linear charge density λ1 and radius a inside a hollow cylindrical pipe of inner radius b and outer radius c and uniform linear charge density λ2. A cross-sectional view of the system is shown below(linked and attached). Find the electric field everywhere and determine the electric potential everywhere, taking the outer surface of the pipe as the zero for the potential.
Homework Equations
/The attempt at a solution[/B]I easily enough determined through Gauss's Law the Electric field from r=0 to r=a, using E*A = Q/ε0 to find E = (λ1*r)/(2ε0) and from r=a to r=b as E = (λ1*r)(a2)/(2*ε0*r). My question lies within the dealing of a non-shell hollow cylinder, and how I find the field produced within and outside of the area from r=b to r=c. My initial thought was that within the outer thick shell would be E = (λ2*r)/(2ε0) + (λ1*r)(a2)/(2*ε0*r), and outside the shell (r>c) would be E = (λ1*r)(a2)/(2*ε0*r) + (λ2*r)(c2)/(2*ε0*r). However, I feel like this doesn't necessarily cover all of my bases, since I feel like I am neglecting the b term. Should the E from the outer thick shell use (c-b)2 rather than just the c term? I think that would make more sense. I haven't tackled the potential portion yet, I feel that would be easier after I determine the field everywhere. Thanks for the help, this is my first time on the site.