Aryamaan Thakur
- 11
- 2
- Homework Statement
- To find the electric potential at the edge of a thin circular plate of radius R carrying uniformly distributed charge of surface density σ
- Relevant Equations
- dV = (1/4πε) dq/r
l = rθ
My question might sound stupid to you but please clear my confusions.
I'm taking an circular arc like element on the plate. That arc has a radius of 'r' (AB) and the radius is inclined at an angle 'θ' with OA (∠OAB).
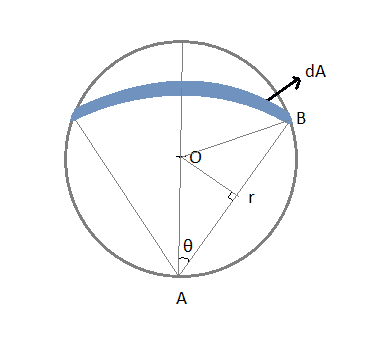
The area between arc of radius r and r+dr is dA.
dA = 2θr.dr
The charge on this area will be dq
dq = σ dA = 2σθr.dr
From ΔAOB, the relation between r and R is:
r = 2Rcosθ
taking derivative on both sides gives:
dr = -2Rsinθ
Potential due to this area at edge A is dV
dV = (1/4πεr) dq = (1/4πε) (-4σRθsinθ.dθ)
So, V comes out to be ∫ dV = (-σR/πε) ∫ θsinθ.dθ
taking limits from 0 to π/2, the integral gives 1
V = (-σR/πε)
I got the right magnitude but wrong sign. Some resources on internet say I should integrate from π/2 to 0.
What is the problem in integrating from 0 to π/2? Why am I getting a negative sign? And why should I integrate from π/2 to 0?
I'm taking an circular arc like element on the plate. That arc has a radius of 'r' (AB) and the radius is inclined at an angle 'θ' with OA (∠OAB).
The area between arc of radius r and r+dr is dA.
dA = 2θr.dr
The charge on this area will be dq
dq = σ dA = 2σθr.dr
From ΔAOB, the relation between r and R is:
r = 2Rcosθ
taking derivative on both sides gives:
dr = -2Rsinθ
Potential due to this area at edge A is dV
dV = (1/4πεr) dq = (1/4πε) (-4σRθsinθ.dθ)
So, V comes out to be ∫ dV = (-σR/πε) ∫ θsinθ.dθ
taking limits from 0 to π/2, the integral gives 1
V = (-σR/πε)
I got the right magnitude but wrong sign. Some resources on internet say I should integrate from π/2 to 0.
What is the problem in integrating from 0 to π/2? Why am I getting a negative sign? And why should I integrate from π/2 to 0?