- #1
StephenDoty
- 265
- 0
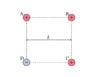
If you calculate W, the amount of work it took to assemble this charge configuration if the point charges were initially infinitely far apart, you will find that the contribution for each charge is proportional to {kq^2}/{L}. In the space provided, enter the numeric value that multiplies the above factor, in W. (See Picture Below)
delta U= -W
delta U= q*delta V
I tried using this idea but my answers are wrong. Like for charge A I got delta V= kq/sqrt(2)*L
or delta U= kq^2/sqrt(2)*L thus W = -kq^2/sqrt(2)*L
But the work for charge A equals 0. So what am I doing wrong?
Thanks
Stephen
delta U= -W
delta U= q*delta V
I tried using this idea but my answers are wrong. Like for charge A I got delta V= kq/sqrt(2)*L
or delta U= kq^2/sqrt(2)*L thus W = -kq^2/sqrt(2)*L
But the work for charge A equals 0. So what am I doing wrong?
Thanks
Stephen