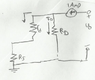
GreenPrint said:
Well if r_{d} is connect to the source then the small signal equivalent circuit for a voltage diver unbypassed R_{S} is exactly the same as the small signal equivalent circuit for a self-bias configuration unbypassed R_{S} if we treat R_{Th} as R_{G}
The formula for the output impedance Z_{O} for a self-bias configuration unbypassed R_{S} is
Z_{O} = \frac{1 + g_{m}R_{S} + \frac{R_{S}}{r_{d}}}{1 + g_{m}R_{S} + \frac{R_{S} + R_{D}}{r_{d}}}R_{D}
if we take the limit
Z_{O} \stackrel{lim}{r_{d} → ∞} = \stackrel{lim}{r_{d} → ∞} \frac{1 + g_{m}R_{S} + \frac{R_{S}}{r_{d}}}{1 + g_{m}R_{S} + \frac{R_{S} + R_{D}}{r_{d}}}R_{D} = R_{D}
Am I really suppose to go with this as the output impedance Z_{O}?
The solutions manual from a previous version has this for the answer.
http://imageshack.com/a/img14/6652/3jn9.png
I know it could be a different problem but it looks like the same exact problem with a different value for r_{d}
The purpose of taking limits is not to find Zo, or that Zo is RD.
You had two possible expressions for Zo. One way to tell which is correct is this:
You know what Zo would be if there were no rd; it would be just RD. So whatever expression you come up with, it must reduce to just RD if you take the limit of the expression when rd→∞.
The second expression's limit is \frac{R_{D}}{1 + g_{m}R_{S}}, which is
not just RD.
The first expression's limit
is just RD.
These two limits don't prove that the first expression is correct; they prove that the second expression is wrong. So, if you knew that the correct answer was one of the two expressions, taking these limits rules out the second one. This is just an aid, like checking units, to help you rule out a wrong result.
Now, if we substitute numerical values into the expressions, we get:
and:
The numerical evaluations are very different; the second is not even a very good approximation to the first.
Have you tried analyzing the circuit to determine Zo? rude man already suggested that you inject a test signal at the output node.
If you set up the KCL equation(s) and inject a 1 amp signal at the output node, the voltage there will be numerically equal to the impedance there. Do it symbolically and substitute numbers once you have a symbolic expression for Zo.