JulienB
- 408
- 12
Homework Statement
Hi everybody! I would like to clear up some doubts I have about my electromagnetism homework:
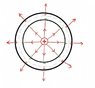
A positive point charge ##q## is placed in the center of an ideal conducting electrically neutral spherical shell, as shown in the attached picture.
a) Calculate the electrical potential ##\phi(\vec{r})## in all locations, that is ## r < a ##, ##a < r < b## and ##r > b##.
b) Sketch the result.
Homework Equations
Gauss's law, equation for electrical potential
The Attempt at a Solution
First I have been attaching a second picture showing how I understand the situation. I think the point charge at the center attracts at the inner border of the shell its negative equivalent of charge and repelling the same amount of positive charge to the outer border. Is that a correct assumption? If yes, I assume there is an electric field going from the point charge ##q## towards the inner border of the shell and from the outer border of the shell outwards (as indicated in the picture).
Now for the math:
- For the case ## r_1 < a ## :
##\oint \vec{E} \cdot d\vec{A} = \frac{q}{\varepsilon_0}##
##\iff E \int dA = \frac{q}{\varepsilon_0}##
## 4 E \pi r_1^2 = \frac{q}{\varepsilon_0}##
## E = k \frac{q}{r_1^2}##
##\implies \phi (\vec{r}) = - \int_{\infty}^{r_1} \vec{E} \cdot d\vec{s}##
## = kq \int_{\infty}^{r_1} \frac{-1}{r^2} ds##
## = \frac{kq}{r_1}##
Is that correct? I'm not sure about the boundaries of my integral, since the path goes through the shell then.
I will wait for an answer before posting the two other results :)
Thanks a lot in advance for your answers!Julien.